Solution to MP64
December 2006

The problem:
            For the holiday season we offer a mathemagical party trick to amaze friends and relatives. No special training is required — just a table and 45 coins. 

Place your 45 coins on the table and ask for a volunteer to blindfold you (this step is optional) and then to arrange the coins in as many piles of whatever height he wishes. He could, for example, make one pile of 24 coins, one of 20 coins, and one of 1 coin. Tell him to take one coin from each of his piles to make a new pile. (In our example the new pile would have 3 coins and the two old piles that remain would now have 23 and 19 coins.) Instruct him to repeat the process — that is, he should take one coin from each pile (including the new) to form a yet another pile (this gives piles of 22, 18, 3, and 2 in our example) — and to keep repeating it.  After a suitable length of time, depending on the starting configuration and the skill of your volunteer, you announce that he has one pile of each size from 1 to 9.
Our problem for December: Prove that this trick always works.

Our problem is based on a game called Bulgarian Solitaire.  Martin Gardner popularized it in his column, "Mathematical Games" [Scientific American 249 (August 1983) pages 18-21].  We thank Philippe Fondanaiche for this information.  He helps run Diophante (www.diophante.fr), a web page devoted to mathematical recreations.  Bulgarian solitaire was the subject of their problem H101; a solution has recently appeared there.  He also directed us to a web page http://www.augsburg.edu/math/faculty/doree/bulgarian_solitaire_bib.pdf that contains more than a dozen references that were inspired by the Gardner article.  Further information can be found in the Wikipedia article http://en.wikipedia.org/wiki/Bulgarian_solitaire. 

We received correct solutions from:  

Philippe Fondanaiche (France)		Sébastien Dumortier (France)
Patrick LoPresti (USA)

Fondanaiche sent us his own solution that is based on one of the references above.  It can be found in full on our French page.  We also received a solution from Sébastien Dumortier that uses a computer to exhaust all possibilities.  His based his approach on the idea that the number of possible ways to arrange the coins in various size piles is equal to the number of partitions of 45 (that is, the number of ways of writing 45 as a sum of positive integers), which happens to be 89134 different ways.  To give you an idea of what is involved, here is the game tree for six coins (instead of 45).  The number 6 has just 11 partitions, so that Bulgarian solitaire played with 6 coins comprises 11 possible states.

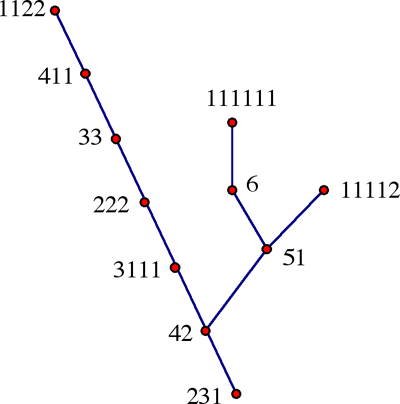
The diagram tells us that if we start with 6 coins in piles of size 1, 1, 2, and 2, then it will take 6 moves to arrive at the steady state with piles of 1, 2, and 3 coins. We present Lo Presti's solution to the general problem, which we have expanded and provided with new notation. It is much easier than anything we have seen in print or on the web.

LoPresti's solution.
            Place the coins on integer lattice points of the xy-plane so that the bottom coins of the piles lie along the x-axis (y = 0), and the first pile extends up the y-axis (x = 0).  We denote by H(j) the y-coordinate of the position of the top coin in the pile above the coin at (j, 0) (so that H(j) equals one less than the height of that pile).  Thus,
            Pile 1 consists of coins at (0, 0), (0, 1), (0, 2), ..., (0, H(0))
            Pile 2 consists of coins at (1, 0), (1, 1), (1, 2), ..., (1, H(1))
            ...
            Pile n consists of coins at (n-1, 0), (n-1, 1), (n-1, 2), ..., (n-1, H(n-1)).

            The transformation to the next state is done in this way:

The bottom coins (0, 0), (1, 0), ..., (n, 0) in that order become the
new Pile 1, (0, 0), (0, 1), ..., (0, n).
Each of the other coins is shifted one unit to the right (to make room for the new left pile) and one unit down (because the bottom coin of each pile was removed).  Also it may happen that some piles became empty, while piles to the right of them are still nonempty.  In that case some nonempty piles will be shifted to the left, so that the nonempty piles are neatly stacked without gaps.  Here is diagram of how the game proceeds when one starts with N = 6 coins (instead of N = 45 coins as in our problem):

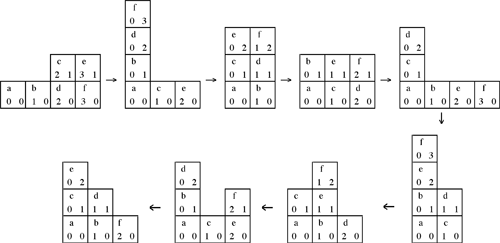
We define the weight of the coin C at position (x, y) to be W(C) = x + y.  The transformation will not alter W(C) if C is shifted from (x, 0) to (0, x) or from (x, y) to (x + 1, y – 1); W(C) will decrease if and only if C is at y = 1 or higher on a pile that is shifted to the left.  So after some iterations every coin C will have attained its minimal weight, and will be shifting down from (0, H(C)) to (H(C), 0) by unit steps, (x, y) (x + 1, y – 1), then back up to (0, H(0)).

CLAIM.  After all coins have reached their minimal weights, if the line x + y = k has at least one coin C then the line x + y = k – 1 must contain a complete set of k coins. 

To prove the claim, we suppose to the contrary that a position of x + y = k – 1, denoted , is missing its coin.  The motion of C has period k + 1 while the motion of  has period k, whence on some move  will be directly below C, which would contradict Newton's law of gravity.
            So let us count coins in the case where k = 8 is the largest weight.  Remember that we start with 45 coins.  We have j + 1 coins on each line x + y = j from j = 0 up to j = 7, and at most 9 coins on x + y = 8.  With k = 8, then 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36; it follows that x + y = 8 must also contain a full set of 9 coins in order for the grand total to be 45.  This arrangement, of course, forces the first pile to contain 9 coins, the next pile 8, and so on down to 1, as desired.

Further comments.
            The reader no doubt will have noticed that our argument works for any number of the form

.

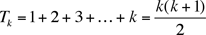These are the triangular numbers (T1 = 1, T2 = 3, T3 = 6, ...).  Whether or not the number of coins N is a triangular number, it is clear (since there are only finitely many possible arrangements) that for any arrangement of N coins into piles, a game of Bulgarian solitaire will eventually end in a cycle of pile sizes that keep repeating.  Our argument applied to a starting arrangement of N coins when N is not a triangular number leads to a theorem of J. Brandt ["Cycles of Partitions", Proc. Amer. Math. Soc. 85 (1982) 483-486] that describes the patterns that repeat.

THEOREM. If N satisfies Tk-1 < N < Tk for the consecutive triangular numbers Tk-1 and Tk, then the arrangement of coins will cycle once the number of coins in pile j (for j = 1, ... , k) is that of either Tk, namely k + 1 – j, or one less than that number.  Furthermore, the number of distinct arrangements in the cycle is a divisor of k.

So, for example, starting with N = 12 coins, we have k = 5 (that is, T4 = 10 < N = 12 < T5 = 15).  An arrangement that will repeat will have the first pile with 4 or 5 coins, second with 3 or 4 coins, third with 2 or 3 coins, fourth with 1 or 2 coins, and fifth with 0 or 1, as long as those numbers sum to 12.  The cycle of five arrangements that contains 5, 4, 2, 1, and the cycle of five that contains 5, 3, 3, 1 produce the ten arrangements that satisfy the theorem.

         In "Solution of the Bulgarian Solitaire Conjecture" [Math. Magazine 58:5 (November 1985) 259-271] Kiyoshi Igusa proves that when N = Tk, a game of Bulgarian solitaire reaches its repeating arrangement in k(k – 1) moves or less.  He can prove that the statement is true for any N < Tk, but he does not know the best possible bound unless N = Tk.  We do not know yet whether one can determine these bounds using our approach.