|
Solution for Summer 2008
| The Problem: |
 |
Summer 2008
Instead of a monthly problem we offer you, for your enjoyment, a summer puzzle in the form of a sequel to Charles Perrault's classic tale "Le petit poucet" (translated into English as "Hop o' My Thumb"); the original is available for downloading from the Gutenberg Project in French or in English: http://www.gutenberg.org/browse/authors/p#a7137. Please send us your solution only if you can PROVE that it is the UNIQUE solution that will save the brothers. The solution will be published at the beginning of September.
The reading of the will was an occasion for the seven brothers to gather once again and reminisce about their childhood. Some memories were pleasant, but others were terrible and painful. There was the time when their parents had tried to lose them in the forest, and they had found their way again only because of the pebbles that the youngest had dropped along the way. Another time they had to run from a frightful ogre.
Now their parents had passed on, and predictably the seven brothers inherited the little old house in the woods where they had been born. However the testament also revealed a considerable surprise: Under the coal bucket in the cellar they were to find the key to the old chest sitting just beside it. Inside the chest they were to find the treasure that their parents had been saving for them.
So the seven brothers went to the cellar of the old house. The oldest lifted the coal bucket, and just then a clanking sound was heard, and a door slammed shut behind them. It was a heavy safe door with a strange combination lock of nine number dials arranged in a 3 by 3 square. They were trapped in the cellar. Nonetheless, the key was indeed under the bucket. When they opened the chest, a rat jumped out, and the brothers discovered that it contained only a short letter and a scrap of newspaper that the rat had been nibbling on. The letter was the last message from their parents:

The brothers frantically went back to the chest. They retrieved the scrap of paper, and to their dismay they discovered that the rat had chewed off the bottom left corner of the sudoku puzzle which was now their only chance of survival.
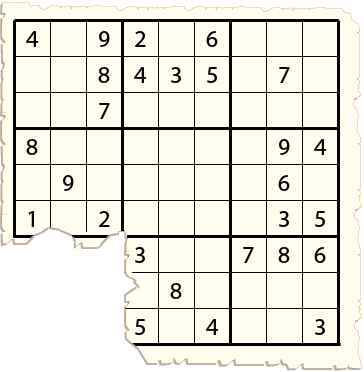
Fortunately, they were all of them avid sudoku players. They copied the puzzle sevenfold, in the hope that at least one of them would still find the solution. Then they started to work on it. The youngest brother had always been the quickest, but on this occasion he was remarkably slow. He would write down a few numbers, then pause for long meditations, while his older siblings scribbled frantically. Indeed in a matter of minutes, the six put down their pens and shouted "I've got it''. But then they compared their solutions, and found out that they were all considerably different. All solutions had the digits 1 through 9 appearing exactly once in every row, column and three by three square, but with the bottom left corner eaten by the rat, there was no way to tell which of their solutions was the correct one, if indeed any one was. At that point they felt sure that they were doomed and started to cry.
But then the youngest brother asked them to give him a little more time to concentrate, so he could find the correct solution. So for a few agonizing minutes, they watched him stare at the puzzle, tap his fingers, stare at the wall and write down a few numbers. When at last he produced his solution, the older brothers found that it was different from all of theirs. They could not tell why his solution was any better than any of theirs. But, he was the youngest, he was the brightest, they had trusted his judgment many times and, indeed, they had survived their childhood mostly because of that. So they set the number dials on the door to match the middle 3 by 3 square in the youngest's solution, pulled the handle and ···
Dear readers, we break off our story here and wish you a pleasant summer. We will post the ending in September. If you can guess how the story ends, you can send us, at The Problem of the Month, your ending with a complete justification.
|
The solution:
. . .The door opened and the seven brothers rushed out of the cellar, out of
the house, through the woods to a clearing where they ducked just as the house
blew up behind them. They had escaped just in time.
When at last they recovered their breath, they noticed that each of them
had kept the scrap of paper on which they had tried to solve the sudoku puzzle.
By then they realized that their younger brother must have known something
that they didn’t, and asked him how he solved the puzzle. This is what he said:
“Before the rat destroyed the bottom left corner, the puzzle must have looked
something like this:
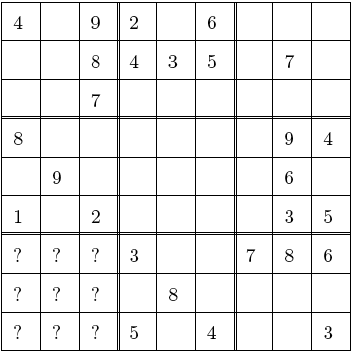
Some of these question marks were blank cells, but others were numbers in
the original puzzle, which forced a unique solution to the problem (as told in the
letter). With these number removed, the puzzle did not become impossible; on
the contrary, we found out that many solutions are now possibles. My challenge
was to find the unique solution of original puzzle among the many possibilities
of the new grid. I had to avoid making guesses, and fill in a number in a cell
only when I knew for sure that it MUST go there because of one of the following
reasons:
- All the other numbers are known to appear elsewhere in the same row,
column or three by three square.
- This number cannot appear elsewhere in the same row, column or three
by three square.
With these rules, I could fill the grid partially, as follows:
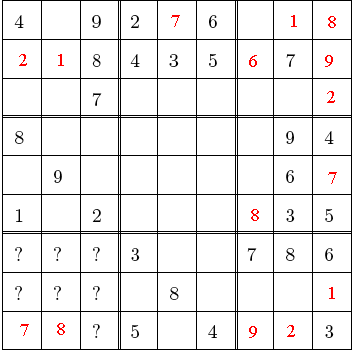
All of your solutions agree with mine up to this point. But this was as far as
I could go without making guesses. Had the bottom left square been intact,
I may have been able to continue in this way, and not only find the unique
solution, but also PROVE that my solution were indeed the unique solution
of the original puzzle. With the bottom left corner destroyed, this option was
gone. So, I had to resort to an unconventional method. I used the uniqueness
of the original solution as an HYPOTHESIS, rather than trying to prove it:
Only the 3, 4, 5 are missing in the top right square, and only the 4 and 5 are
missing the bottom right square. The top 3 goes in column 7, either in row 1
or row 3. Could the 3 go in row 1? There is no apparent contradiction; indeed,
one of your solutions has the 3 in row 1. But in this case the fours and fives of
rows 3 and 8 appear in some order in columns 7 and 8, and we get a SECOND
solution by interchanging them. However we know that the original puzzle had
a unique solution. This means that the missing bottom left corner contained
information which at some point would have blocked the 3 from appearing in
row 1, column 7. Therefore there must be a 3 in row 3, column 7.
This in turn allowed me to fill the puzzle a little more, by putting in the 3
in the top left corner, then completing the top right and bottom right squares.
Afterwards the puzzle looked like this.
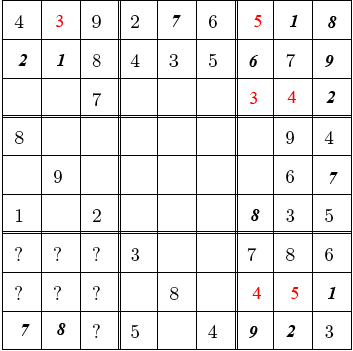
I then turned to the top left square, which could be completed by putting
in the 5 and the 6 in some order in the two empty cells. Again I found no
contradiction in putting the 5 in row 3, column 2, (indeed one of your solutions
has the 5 there), except that it would lead to a second solution obtained by
interchanging the 3 and the 5 in the top left and top right squares. So, I
concluded that the original bottom left square would at some point have ruled
out the 5 in this position, and put the 5 in row 3, column 1, and a 6 in row 3.
At this point I was able to fill in the puzzle a lot more:
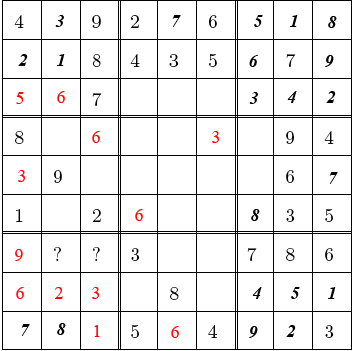
Only the 4 and the 5 were missing in the bottom left corner. I noticed that
by putting the 4 in column 2 and the 5 in column 3, I got multiple solutions.
So, they had to go the other way around. At that point I had reconstituted the
original bottom left corner, and I could complete the original puzzle.”
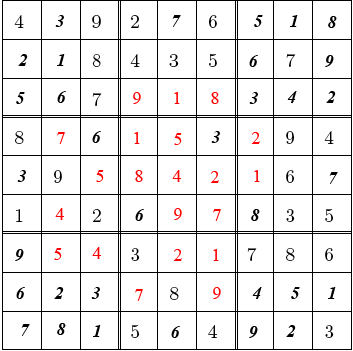
So, this is how Hop o’ My Thumb saved his family one more time. The seven
brothers went back to see the remains of the house. Everything was destroyed
and there was nothing left to salvage, not a bonnet, not a breadcrumb and not
even a feather. So, they parted ways again and returned to their lives with their
newfound bit of wisdom, which is indeed worth more than treasures of gold and
diamonds.
Comments In “Sudoku squares and chromatic polynomials” [Notices of the
Amer. Math. Soc., 54 (2007) no. 6, 708-717], A. Herzberg and R. Murty link
Sudoku puzzles to graph colouring. Our summer problem was inspired by an
application of the “Kempe chain argument” to Sudoku puzzles. This argument
was introduced by Kempe in his 1879 attempt to prove the famous 4-colour
problem which states that four colours always suffice to colour the countries in
a map so that neighbouring countries get different colours. However, Kempe’s
argument was incomplete, and the four colour problem remained open until
complete proofs were given by Appel and Hacken in 1976 and by Robertson,
Sanders, Seymour and Thomas in 1996.
We received complete solutions to our problem from Philippe Fondanaiche
(France), Minghua Lin (China), Jerry Powidajko (Canada), Gérard Billion
(France), Jose Arraiz (Brazil), Jacques Mertzeisen (France), Patrick J. LoPresti
(USA), Zachary Friggstad (Canada), Matthew Lim (USA) and Bojan Basic (Serbia). Like the modern solvers of the four colour problem, most of our solvers used computers and showed that with the bottom left corner chewed out, the puzzle had 26 solutions. We provide a link below to Friggstad’s solution and program, to
Fondanaiche’s computer-free solutions and to Lim's computer-free solution and computational solution using Donald Knuth's "dancing links X" algorithm.
|

