Solution to MP70
September 2007
The problem:
Six points have been arranged so that the 15 segments that join them in pairs have different lengths and point in different directions. Prove that one of these segments is the longest side of one of the triangles that are formed and, at the same time, the shortest side of another triangle. Is the same claim true when starting with five points (and the 10 segments joining them in pairs have different lengths and different directions)?
Correct solutions came from Philippe Fondanaiche (France), Wolfgang Kais (Germany), John T. Robinson (USA), and K. Sengupta (India). Most noticed the relationship of our problem to the Ramsey number R(3, 3). An elementary solution in the language of Ramsey theory can be found in many reference books. John Robinson told us about the particularly nice solutions on the web pages
http://www.cut-the-knot.org/Curriculum/Combinatorics/ThreeOrThree.shtml,
and
http://en.wikipedia.org/wiki/Ramsey's_theorem.
We took our version of the problem from Mathematical Miniatures by Svetoslav Savchev and Titu Andreescu [published in 2003 by the Mathematical Association of America].
Here is the solution from Kais, somewhat modified:
The given conditions insure that any three of the points form a triangle with one shortest, one medium, and one longest side. (It is clear that the points and lines could be replaced by the 6 vertices and 15 edges of a complete graph, with different numbers assigned to each edge, but we will stay with the language of geometry.) Colour a segment red if it is the shortest side of at least one triangle, and colour all other segments blue. Because every triangle has a shortest side, we deduce that
(*) the configuration contains no blue triangle.
Let us look at one of the points P and the five segments that connect it to the other points. Since they are either red or blue, we know (from the pidgeonhole principle) that
(A) three or more of the segments from P are red,
or
(B) three or more of the segments from P are blue.
In either case, the configuration has a red triangle: Should (A) hold then the other three endpoints of the red segments form a triangle with at least one red side (because of *); this side together with the two adjacent red sides connected to P form a red triangle. On the other hand, should (B) hold, then (*) implies that none of the segments connecting two of the three other endpoints of the blue lines from P can be blue, so those three segments form a red triangle.
The red triangle we have found corresponds to three segments connecting three points, where each segment appears as the shortest side in at least one of the 20 triangles of the configuration. Of course, this triangle contains a longest side which, because it is red, is at the same time the shortest side of some triangle.
Comment. We did not use the minimality of a shortest side in the argument. Since every triangle contains exactly one shortest, one longest, and one medium-length side, our argument shows that at least one of the 20 triangles consists of three sides that each appear as the shortest side of some triangle, at least one of the triangles consists of three sides that each appear as the medium-length side of some triangle, and at least one of the triangles consists of three sides that each appear as the longest side of some triangle.
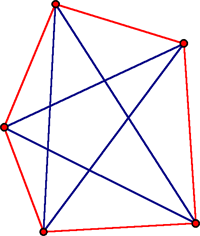
To see that the claim is not true starting with five points, perturb the vertices of a regular pentagon slightly so that the five sides are all of different lengths as are the five diagonals. This can be accomplished so that the shortest of the diagonals remains longer than the longest of the sides. This means that no triangle determined by these five points would have three sides Five points can be arranged so that five of the segments joining pairs of the points are each the shortest side of some triangle and never the longest, while the five segments joining the remaining pairs of points are each the longest side of some triangle and never the shortest.

