|
Solution for April 2008
| The Problem: |
 |
MP77 April 2008
Let a, b and c be positive integers whose only common divisor is 1 — that is, no integer greater than one divides all three — for which
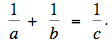
Prove that (a + b), (a – c) and (b – c) are all perfect squares.
|
Correct responses: |
 |
This month's problem came from Problem of the Week number 1094 (March 27, 2008), run by Andrew Beveridge at Macalester College in St. Paul, Minnesota; their source was School Science and Mathematics 63 (October 1963), p. 60.
Correct solutions were submitted by
Bojan Basic (Serbia) |
Wolfgang Kais (Germany) |
Gérard Billion (France) |
Normand LaLiberté (Ontario) |
Lou Cairoli (USA) |
Matthew Lim (USA) |
John Campbell (Alberta) |
Richard McIntosh (Regina) |
Olivier Cyr (France) |
Jacques Mertzeisen (France) |
Dan Dima (Romania) |
Giovanni Parzanese (Italy) |
Philippe Fondanaiche (France) |
Ananda Raidu (India) |
Mudit Goel (India) |
John T. Robinson (USA) |
Xavier Hecquet (France) |
K. Sengupta (India) |
|
A. Teitelman (Israel) |
We also received three partial solutions. |
The solution:
First multiply both sides of 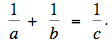 by abc to get by abc to get
(a + b)c = ab. (1)
Moreover, we are told that the only positive divisor of a, b, and c is 1, which we write
gcd(a, b, c) = 1. (2)
If we denote the greatest common divisors of pairs of the given integers by
d = gcd(a, b), e = gcd(a, c), and f = gcd(b, c),
the solution to our problem will come down to showing that a + b = d2, a – c = e2, and b – c = f2. Our correspondents deduced this using a variety of arguments; here are the two most popular approaches. We will follow them by a third approach that yields Fermat's Last Theorem for negative exponents as a by-product.
Method 1.
Equation (1) implies that ac < ab and bc < ab, so that c is smaller than either a or b, whence
r := a – c and s := b – c
define two positive integers. We substitute a = r + c and b = s + c into (1) to get (r+c+s+c)c = (r+c)(s+c), which simplifies to
c2 = rs. (3)
Let k be a common divisor of r and s. From (3) k divides c, which implies that k also divides a = r+c and b = s+c, so that (because of (2)) k must be 1. In other words, r and s are relatively prime. Consequently, (3) now implies that r = a – c and s = b – c are perfect squares, as desired. (Details: From (3), any prime factor of c is also a prime factor of exactly one of r or s, and conversely; since any prime appears as a factor of c2 an even number of times, it must appear the same number of times as a factor of r or of s.) It remains to show that a+b is also a perfect square. But this follows quickly from applying (1) to what we have already established:
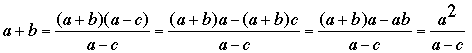
which is an integer written as the quotient of two squares, so that it is likewise a square, as claimed.
This completes the argument, but our proof provides further information:
Since a – c and b – c are perfect squares, we can write them as
r = a – c = u2 and s = b – c = v2, u,v > 0, gcd(u, v) = 1.
It follows from (3) that c = uv; thus, we can characterize all triples of integers a, b, and c for which gcd(a, b, c) = 1 and
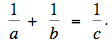
There is a bijective correspondence between the triples (a, b, c) and pairs of relatively prime positive integers u and v for which
a = u(u + v), b = v(u + v), and c = uv.
So, for example, the choice u= 2 and v = 5 gives us 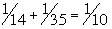 . .
Method 2.
Recall that we have defined d = gcd(a, b), e = gcd(a, c), and f = gcd(b, c). We first observe that each pair of d, e, f is relatively prime as a consequence of (2). For example, gcd(d, e) = 1 because any divisor of d would necessarily divide a and b, while any divisor of e would necessarily divide a and c; consequently any divisor of both d and e would divide all of a, b, and c, and therefore have to equal 1. Next, any prime divisor of a would divide the right side of equation (1), so that it would necessarily divide either (a+b), and therefore it would divide b, or else it would divide c; however, because of (2) that prime divisor of a could not divide both b and c. In other words,
All prime divisors of a necessarily also divide exactly one of b or c.
This implies that every prime divisor of a divides exactly one of d or e, whence
a = de.
Similarly, we get
b = df and c = ef.
Substituting these values of a, b, c into (1) we get, (de + df)ef = d2ef, whence
e + f = d.
Our desired result follows immediately:
a + b = de + df = d(e + f) = d2
a - c = df - ef = e(d - f) = e2
b - c = df - ef = f(d - e) = f2
Method 3 (Richard McIntosh).
Dividing xn + yn = zn by (xyz)n yields (yz)-n + (xz)-n = (xy)-n We consider multiples of solutions to be equivalent and write (x,y,z) ∼ (kx,ky,kz), where k ε Q -{0}.
Define
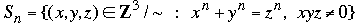
and
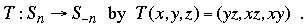
[Comment: for those readers who are not used to this fancy notation, we need it only for technical reasons. You might prefer to skip to the end and see how an example works. Meanwhile, you can simply consider triples such as (3, 4, 5) and (6, 8, 10) to be the "same" Pythagorean triple since both 32 + 42 = 52 and 62 + 82 = 102, and each is a multiple of the other. Note that T takes (3, 4, 5) to (20, 15, 12), and the latter is taken by T to (180,240,300) = (60·3, 60·4, 60·5) ~ (3, 4, 5).]
Since T(T(x,y,z) = (x2yz, xy2z, xyz2) ~ (x,y,z), it follows that T is a bijection. By a straightforward argument one shows that if gcd(x,y,z) = 1, then gcd(yz, xz, xy) = gcd(x,y)·gcd(x,z)·gcd(y,z).
Suppose n = 1 and x + y = z. If gcd(x,y,z) = 1, then gcd(x,y) = gcd(x,z) = gcd(y,z) = 1, whence (from the previous paragraph) gcd(yz, xz, xy) = 1. Therefore all solutions of 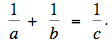 that satisfy gcd(a, b, c) = 1are of the type that satisfy gcd(a, b, c) = 1are of the type
(a, b, c) = (yz, xz, xy) with x + y = z and gcd(x,y,z) = 1. As a consequence,
a + b = yz + xz = (x+y)z = z2 = [gcd(a,b)]2,
a – c = yz – xy = (z – x)y = y2 = [gcd(a,c)]2, and
b – c = xz – xy = (z – y)x = x2 = [gcd(b,c)]2.
There are two simple consequences of Method 3.
- We have here a second characterization of the solutions — for each pair of relatively prime integers x and y, we set z = x + y. This gives us the triple a = yz, b = xz, c = xy. Thus, corresponding to the example we worked at the end of Method 1, we take x = 2 and y = 5, so that z = 2 + 5 = 7. Divide this sum by 2·5·7 to get
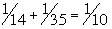 . .
- Our argument leads to an interesting result:
Corollary. There exist nonzero integers a, b, and c for which an + bn = cn if and only if n is 1, 2, –1, or –2.
Proof. The hard part of the proof comes courtesy of Fermat and Wiles, who eliminated the cases n ≥ 3. Our argument above establishes that there is a solution for an integer n if and only if there is a solution for –n.
|

