|
Solution to MP71
October 2007
The problem:
A circle with center O and radius 1 cm rolls around the inside of a triangle whose sides are 6, 8, and 10 cm, always touching one or more of the sides as it rolls. How far does O travel in one complete circuit?
This month's problem was taken off a list of practice problems from the 2002 Waterloo Mathematics Contests Seminar. Correct solutions were submitted by
Felix Arnaiz Lanzo -- 2 solutions (Spain) |
Matthew Lim (USA) |
Gérard Billion (France) |
Jacques Mertzeisen (France) |
Ritwik Chaudhuri (India) |
Kacem Nouini (France) |
Sébastien Dumortier (France) |
Mark Pilloff (USA) |
Baptiste Gorin -- 2 solutions (France) |
John T. Robinson (USA) |
Xavier Hecquet (France) |
K. Sengupta (India) |
Normand LaLiberté (Ontario) |
A. Teitelman (Israel) |
Farid Lian Martínez (Spain(?)) |
Philippe Fondanaiche (France) |
Solution. All solvers first note that as the circle rolls around the given triangle, ABC say, its centre O stays a distance of one cm from the side along which it moves. The centre's path is therefore a triangle, call it A'B'C', whose sides are parallel to the sides of ΔABC. The problem becomes finding the ratio of magnification of the dilatation that takes A to A', B to B', and C to C'. Our solvers used a variety of neat ways to determine that the ratio is ½, so that the distance traveled by O is half the perimeter of ΔABC, namely ½(6 + 8 + 10) = 12.
We sample here four of their solutions.
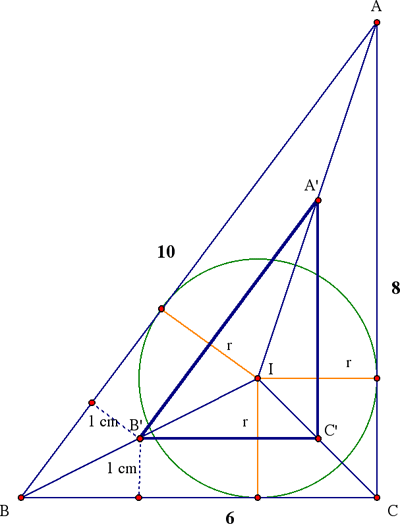
Method 1. This method was the most popular. Because a vertex such as B' of the inner triangle is at an equal distance (namely 1 cm) from the sides BC and BA touched by the rolling circle when centred at B', it lies on the bisector if the corresponding angle at B; thus
AA', BB', and CC' meet at the incentre I of ΔABC,
which is therefore the centre of the dilatation that (1)
takes ΔABC to ΔA'B'C' and, consequently, I is also
the incentre of ΔA'B'C'.
We seek the ratio of the inradii of the two triangles. Denote the inradius of ΔABC by r. Because
(Area of ΔABC) = r · (semiperimeter) = r · ½(6 + 8 + 10 ) = 12r,
and the area is ½(6·8) = 24, we deduce that r = 2. (Comment. Area = r ·(semiperimeter) is a standard result that can easily be seen in the figure above, observing that the area of the big triangle equals the sum of the areas of the three smaller triangles such as IBC that share the vertex I.) Since the inradius of ΔA'B'C' equals r – 1 = 1, the ratio of magnification of the dilatation that takes ΔABC to ΔA'B'C' is ½ as claimed.
Comment. This method applies more generally to a circle of radius r* rolling around a given triangle ABC whose semiperimeter is s and area is F (with F obtained by Heron's formula); then r = F/s, and the ratio of magnification would be (r – r*)/r. Robinson takes this generalization a step further, noting that the same argument works for any n-sided polygon that has an incircle. Of course, for an arbitrary polygon both the area and the perimeter would have to be given.
Method 2 (Billion). As in method 1, we need to find r. We first note that because BC2 + CA2 = 62 + 82 = 102 = AB2,
ΔABC has a right angle at C. (2)
The inradius of ΔABC can be obtained by using the fact that the tangents to the incircle from a vertex have equal lengths (as in the accompanying figure). Because of the right
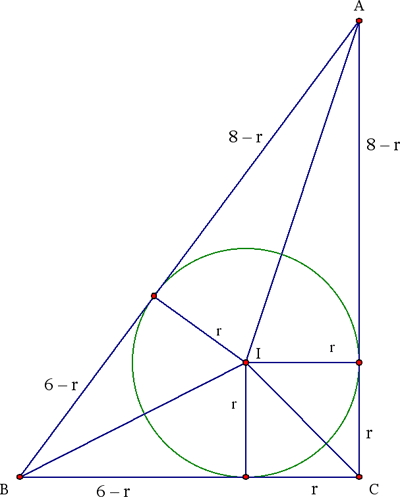
angle at C, the tangents from C have length r. Thus, perimeter = 6+8+10 = 24 equals 2·((6 – r) + r + (8 – r)) = 28 – 2r, so again we see that r = 2.
Method 3. Five of the submitted solutions used (1) together with a trig formula such as
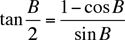
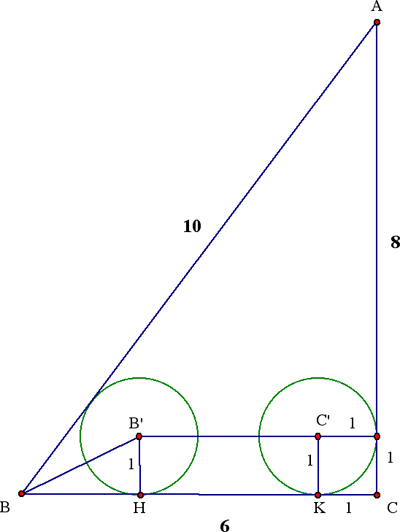
As in the figure, cos B = 3/5 and sin B = 4/5, whence tan (B/2) = 1/2. Since ΔBHB' = B/2 and B'H = 1, we have BH = 2. Together with BC = 6 and KC = 1, we deduce that HK = 3. But then B'C' = HK = 3, and we see that the desired ratio of magnification is
B'C' : BC = 3 : 6 = 1:2.
Method 4. (Nouini's method, modified to emphasize the similarity to Method 3.) We modify Method 3 by using similar triangles instead of trigonometry. The congruent triangles labeled S and T in the figure are similar to ΔABC; with one leg of 1 cm, the
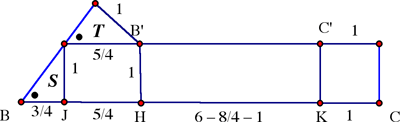
hypotenuse is 5/4 cm and the other leg is 3/4. Thus BJ is labeled 3/4, JH is 5/4, and KC is 1; HK is therefore 6 – 2 – 1 = 3, as in method 3.
|

