|
Solution for November 2007
| The Problem: |
 |
Prove that for every n, the integers 1, 2, 3, ... , 2n – 1, 2n can be partitioned into pairs
{a1, b1}, {a2, b2}, ... , {an, bn}
so that ai + bi is prime for every i.
|
Correct responses: |
 |
Correct solutions were submitted by
Bojan Basic (Serbia) |
Wolfgang Kais (Germany) |
Gérard Billion (France) |
Jeremy Lam (UK) |
Lou Cairoli (USA) |
Jacques Mertzeisen (France) |
John Campbell (Alberta) |
Viktor Pačnik (Slovenia) |
Adrien Delcour (Belgium) |
Mark Pilloff (USA) |
Philippe Fondanaiche (France) |
Ananda Raidu (India) |
Alenka Gabrovec (Slovenia) |
John T. Robinson (USA) |
Xavier Hecquet (France) |
Heri Setiyawan (Indonesia) |
| Pierre Bornsztein (France) |
Luis Fabricio Tano (internet) |
| Jean-Luc Luyet (Switzerland) |
|
|
The solution:
Preliminary remarks. The solution depends on a result that is known variously by the names Bertrand's Postulate (after Joseph Bertrand (1822-1900) who conjectured it in 1845) and Chebyshev's Theorem (after Pafnuty Chebyshev (1821-1894) who proved the conjecture in 1850):
For every integer n > 1, there is at least one prime number
between n and 2n.
Or, in the words of mathematician N.J. Fine,
Chebyshev said it, but I'll say it again;
There's always a prime between n and 2n,
(which rhymes in American English, but probably sounds a bit strange to our British colleagues). Details can be found on the web
http://mathworld.wolfram.com/BertrandsPostulate.html
http://en.wikipedia.org/wiki/Bertrand%27s_postulate
or in standard number theory texts.
All correspondents submitted essentially the same proof. First, we look at a simple example to motivate our argument: Let's partition the numbers from 1 to 8 into pairs, each of whose sum is prime. We note that there are two primes between 8 and 15 that we can aim for, namely 11 and 13. Let's choose 13; the corresponding pairs {5, 8}, {6, 7} sum to 13 and they use up all numbers in the subset from 5 to 8. The task is now reduced to pairing the remaining numbers from 1 to 4. This example should make it clear that an induction argument will be useful here.
Proof by induction. To start the induction, the case n = 1 (with the given integers 1 and 2) is immediate — the numbers already form a pair whose sum is 3, a prime. We next assume that the assertion is true for n running from 1 to k – 1; that is,
assume that for every n from 1 to k - 1, the integers 1, 2, 3, ..., 2n – 1, 2n can be partitioned into pairs {a1, b1}, {a2, b2}, ..., {an, bn} so that ai + bi is prime for every i.
We use the assumption for the case n = k; that is, we must pair the numbers from 1 to 2k. By Bertrand's Postulate we are guaranteed a prime p between 2k and 4k. Since
2k > p – 2k ≥ 1, we can pair
2k with p – 2k,
2k – 1 with p – 2k + 1,
...
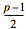 with with 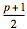 . .
Note that members of each pair sum to p, and all numbers from p – 2k to 2k have been used. Because p – 2k – 1 is an even number that is at most 2(k – 1), the induction hypothesis can now be applied to pair the numbers from 1 to p – 2k – 1, and the proof is complete.
|

