Solution for May 2008

The Problem:
	MP78 May 2008 For which positive integers n can n! be written as a difference of two squares?

Correct responses:

Correct solutions were submitted by Felix Arnaiz Lanzo (Spain) Xavier Hecquet (France) Jose Arraiz (Brazil) Jeff Heleen ((USA) Guillaume Baraston (France) Wolfgang Kais (Germany) Bojan Basic (Serbia) Michael Kozdron (Regina) Luigi Bernardini (Italy) Normand LaLiberté (Ontario) Gérard Billion (France) Farid Lian Martínez (Colombia) Lou Cairoli (USA) Matthew Lim (USA) John Campbell (Alberta) Jean-Luc Luyet (Switzerland) Olivier Cyr (France) Jacques Mertzeisen (France) Dan Dima (Romania) Minghua Lin (China) Sébastien Dumortier (France) Giovanni Parzanese (Italy) Eiden, Jean-Denis (France) John T. Robinson (USA) Philippe Fondanaiche (France) K. Sengupta (India) Bob Franz (USA) A. Teitelman (Israel)             We also received one partial solution.

The solution:

Solution. We first must decide whether or not we wish to restrict our two squares to the positive integers, or whether we wish to allow the value zero — our correspondents were split on the issue.  It matters little since the only value of n! that is a perfect square is n! = 1, in which case 1 = 1 – 0 is the difference of two squares.  (It is easily seen that no other value of n! can be a square; for example, the prime factorization of n! when n ≥ 2 will always contain the first power of a prime greater than n/2.)  For n > 1, people used one, or sometimes both, of two approaches to the answer:

It is possible to express n! as the difference of two perfect squares for all positive integers except n = 2 and n = 3.

The fast approach.
The product of two even numbers can always be expressed as the difference of perfect squares; thus if n ≥ 4 is an integer, we can factor n! as

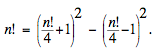
Finally, it is not possible to express 2! = 2 or 3! = 6 as a square because both these numbers are congruent to 2 (mod 4), while all squares must be congruent to 0 or 1 (mod 4), whence their difference can be only 0, 1, or 3 (mod 4).  Alternatively, these two cases can be eliminated by observing that no two small squares (among 0, 1, 4, and 9) admit a difference of 2 or 6, while any other pair of perfect squares must have a difference of 7 or more.
The more informative approach.
Let n be a positive integer and let a and b be integers for which

n! = a² – b² = (a + b)(a – b).

Because a + b and a – b must have the same parity, it follows that n! must be either odd or divisible by 4.  The only odd factorial is 1 (which, we have seen, can be written as the difference of two squares if zero is permitted), while n! is divisible by 4 if and only if n ≥ 4.  Let p > q be two even numbers for which n! = pq, and set

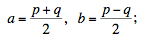
then p = a + b, q = a – b, and n! = pq =  a²– b², as desired.

Further comments.

1. It is clear from the second solution that for n > 1, the number of ways to write n! as the difference of two squares equals the number of pairs (p, q) for which p > q are two even numbers such that n! = pq.  For example, 24 = 2·12 = 4·6; thus, when n = 4, we have (p, q) = (12, 2), (6, 4), and
   
                     4! = 24 = (7 + 5)(7 – 5) = (5 + 1)(5 – 1).
   
         Likewise, 120 = 2·60 = 4·30 = 6· 20 = 10·12; thus when n = 5, (p, q) = (60, 2), (30, 4), (20, 6), (12, 10), and
   
                     5! = 120 = (31 + 29)(31 – 29) = (17 + 13)(17 – 13)
                                   = (13 + 7)(13 – 7) = (11 + 1)(11 – 1).
   
         Alternatively, the number of ways n! can be represented as the difference of two squares equals half the number of positive integer divisors of n!/4.  This observation led John Robinson to develop a simple recursive algorithm to determine that number, which enabled him to produce the sequence
   
                             1, 0 , 0, 2, 4, 9, 18, 36, 60, 105, 210, ... .
   
         His sequence has recently been added to the On-Line Encyclopedia of Integer Sequences.  For details, see
   
                      http://www.research.att.com/~njas/sequences/A138196.
   
         For example, 100! can be expressed as a difference of squares in 19102653480960000 different ways.
   
   
2. Mingua Lin looked at the related problem of expressing n! as the sum of two squares.  The solution is based on the theorem: a positive integer is the sum of two squares if and only if each of its prime factors of the form 4k + 3 occurs to an even power in its prime factorization.  For example,
   
                         6! = 720 = 2⁴ · 3² · 5.
   
         Since 3 is the only prime factor of 720 in the form 4k + 3, and its exponent is even, 720 must be expressible as the sum of two squares; in fact, 720 = 12²(4 + 1) = 24² + 12².  Our conjecture is that 1!, 2!, and 6! are the only possibilities: the prime factorization of n! for larger values of n will have many primes from n/2 to n; their exponent will be 1 (and therefore not even).  It seems reasonable to speculate that at least one of those primes will be in the form 4k + 3.