Solution for February 2008

The Problem:

A vertical plane contains a circle and point P: P lies outside the circle and above the horizontal line that the circle sits on.   Your job is to stretch a thin wire in a straight line from P to a point Q on the circle so that a bead sliding down the wire will reach the circle in the least possible time.  Gravity is the only force acting on the bead.  The shortest path is along a wire that forms part of the line joining P to the circle's centre, while the steepest path would be tangent to the circle. Some path between these two will mix just the right blend of distance and speed, and you have to determine which one it is.                         We all remember from high school that wire and air are frictionless; Newton informed us that the relationship among distance s, velocity v, and time t of a body under constant acceleration is                   s = 1/2vt; and if m is the bead's mass, g is gravity, and h is the vertical component of the drop from P to Q, then the potential energy mgh equals 1/2mv2, where v is the velocity of the bead when it reaches Q.

Correct responses:
	Correct solutions were submitted by Gérard Billion (France), Philippe Fondanaiche (France), Farid Lian Martinez (Colombia), Richard McIntosh (Regina), Jacques Mertzeisen (France), Matthew Lim (USA), Giovanni Parzanese (Italy), John T. Robinson (USA).  The shortest solutions reduced the problem to geometry; we will look at two of them.

The solution:

Geometric method 1.  (Billion, Mertzeisen, Parzanese and Robinson).

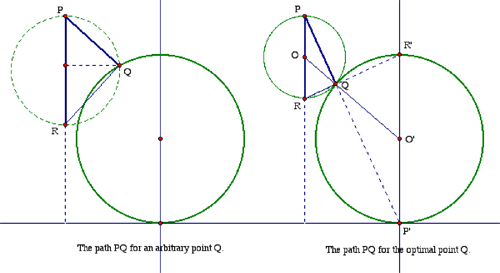
Suppose that two beads are released simultaneously from point P, one sliding down the path from P to its destination Q on the given circle, the other falling vertically toward R.  The force of gravity pulls the beads along so that PQ = PR cos∠RPQ.  The point Q that is attained in the shortest possible time thus corresponds to the highest possible position of the point R.  Because the angle at Q in triangle PQR is a right angle, PR must be the diameter of the circle around PQR.  It follows that the optimal position of Q is obtained when that circle is tangent at Q to the given circle (as seen in the figure on the right).  Let P' be the lowest point of the given circle (where it touches the ground line).

Claim. The point Q for which the path PQ is optimal lies on the line PP'.

The easiest proof of the claim is to observe that that figures of the circumcircle of DPQR (centred at O) and the given circle about triangle P'QR' (centred at O') are homothetic with respect to the point Q.  Alternatively, since the circles are tangent at Q, the line OO' that joins the centres must pass through Q.  Furthermore, because PO || P'O', the alternate interior angles ∠POQ and ∠P'O'Q must be equal; also, the angles at P' and Q in the isosceles triangle P'O'Q both equal 1/2(180^o - ∠P'O'Q) while the angles at P and Q in triangle POQ both equal 1/2(180^o - ∠POQ) In other words, all four of these angles are equal; in particular, ∠PQO = ∠P'QO, whence Q must lie on the line PP' as claimed.

Geometric method 2.  (McIntosh and Fondanaiche).
            Let s = PQ be the distance traveled by the bead, and h = PH be its projection on the vertical PH₁.  As in the accompanying figure, Q₁ is the point where PQ again meets the

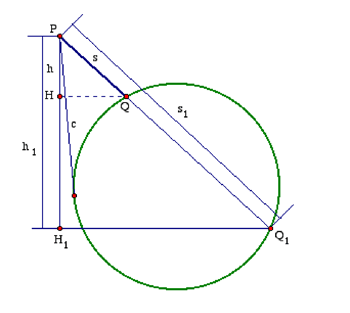
given circle, and H1 is the projection of Q₁ on the  vertical through P.  The law of motion says that the distance s and time t required to travel that distance are related by the formula s = (1/2)at², or

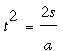
where a = g cos ∠HPQ = g h/s is the acceleration due to gravity along the inclined path PQ. That is,

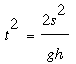
For any location of Q on the circle, the triangles PHQ and PH₁Q₁ are similar, so that s/h = s₁/h₁; also, a basic theorem of Euclid (III.36) says that s·s₁ = c², where c is the length of the tangent from P (which is constant).  Thus

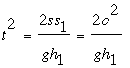
The last equation tells us that t is inversely proportional to h₁ — time is minimized when h₁ is maximized.  We should therefore choose Q so that Q₁ is the lowest point on the circle.

Other solutions.  Both Lim and Lian used calculus for their solution.  It turns out to be a nice exercise in that method, particularly if as Lim did, one chooses the origin to be at the lowest point of the given circle.  Both Robinson and Lian described Q in terms of coordinates with the origin at the centre of the given circle, which obscures, somewhat, its location.