|
Solution to October 2005 Problem
The Problem:
The first player tosses a coin 1001 times while the second player
tosses a coin only 1000 times. What is the probability that the first
player gets more heads? (Please avoid tedious computations here.)
We received correct solutions from
Said Amghibech (Quebec) |
|
Wolfgang Kais (Germany) |
Daniel Bitin (internet) |
|
Arne Loosveldt (Belgium) |
Pierre Bornsztein (France) |
|
Patrick LoPresti (USA) |
K.A. Chandrashekara (internet) |
|
Juan Mir Pieras (Spain) |
| Philippe Fondanaiche (France) |
|
Mark Pilloff (USA) |
| Jeremy Thiesen (internet) |
|
André Gadbois (Quebec |
It is understood that the coins are fair: P(heads) = P(tails) = ½ for each toss.
Method 1. Similar solutions from Bitin, Bornsztein, Fondanaiche, Kais, Loosveldt, LoPresti, and Pilloff.
There are three possible outcomes after each player has tossed his coin 1000 times.
Outcome A: Player 1 flips more heads than player 2.
Outcome B: Player 1 flips fewer heads.
Outcome C: Both players flip the same number of heads.
Since exactly one of these outcomes will occur, P(A) + P(B) + P(C) = 1. Since we assume that the game is fair, it follows that P(A) = P(B) = 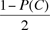 . There are two ways for the first player to have more heads at the end — either outcome A has occurred and he is already ahead after 1000 tosses, or outcome C has occurred (they are tied after 1000 flips) and his final toss is heads. Denote this outcome by H and note that P(H) = ½. The probability that player 1 gets more heads is therefore . There are two ways for the first player to have more heads at the end — either outcome A has occurred and he is already ahead after 1000 tosses, or outcome C has occurred (they are tied after 1000 flips) and his final toss is heads. Denote this outcome by H and note that P(H) = ½. The probability that player 1 gets more heads is therefore
P(A) + P(C)·P(H) =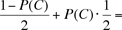 1/2 . 1/2 .
Method 2. Similar solutions from Anghibech, Chandrashekara, and LoPresti.
This solution is based on the almost obvious fact that player 1 either gets more heads than player 2, or he gets more tails — the two outcomes are complementary. (Suggestion. If you find this fact less than obvious, substitute a modified version of the problem in which player 1 flips two coins and player 2 just flips once; you can list all 8 possible outcomes. You will then see clearly that player 1 gets more heads in 4 of these outcomes, while in 3 of the 4 cases where he gets more tails, both players get the same number of heads. The key observation is that the number of throws by the two players differ by one.) Here is an argument to justify our claim: Let Hi and Ti, i = 1, 2, denote the number of heads and tails for player i. Because H1 = 1001 – T1 and H2 = 1000 – T2, H1 > H2 would imply T1 ≤ T2 while T1 > T2 would imply H1 ≤ H2. That is, if player 1 does not get more heads than player 2, then he must get more tails; vice versa, if he does not get more tails, then he must get more heads. Since each of the outcomes "more heads" and "more tails" are equally likely (we get a 1-1 correspondence by interchanging the roles of heads and tails) and no other outcome is possible, the probability of player 1 getting more heads is ½.
Method 3. Generalization by Juan Mir Pieras.
By coincidence, a similar but more general problem appeared last year in the journal Gaceta de la Real Sociedad Matemática Española. Mir's solution that was featured there generalized the journal's problem: If player i flips ni coins and gets Hi heads, then H1– H2 + n2 follows a binomial distribution with parameters n1 + n2 and ½. This means that the probability that player 1 gets k more heads than player 2 is
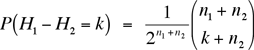 , – n2≤ k ≤ n1. , – n2≤ k ≤ n1.
Note that the distribution of H1 – H2 + 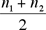 is symmetric about 0. Thus in our problem, n1 =1001, n2 =1000, and is symmetric about 0. Thus in our problem, n1 =1001, n2 =1000, and
P(H1 – H2 ≥ 1) = P(H1 – H2 ≤ 0) = ½.
We have placed Mir's solution (in Spanish) on our Spanish page.
| 
