Solution to September 2005 Problem
The Problem:
Our first problem of the new season deals with integers. As a warm-up exercise after the long summer break you might try to show that for every odd number n, 4n + 1 is a multiple of 5. For the September problem you must
Prove that if the number n is odd and greater than 3 then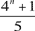 
cannot be a prime number.
We received solutions (which were mostly correct, except for some problems with details, no doubt due to the summer break) from
Said Amghibech (Quebec) |
|
Pierre Bornsztein (France) |
John Campbell (Edmonton) |
|
Xavier Hecquet (France) |
Wolfgang Kais (Germany) |
|
Patrick LoPresti (USA) |
Juan Mir Pieras (Spain) |
|
|
Proof that 4n + 1 is divisible by 5 when n is odd.
One easy way to prove this is to show that the number is congruent to zero modulo 5:
When n is odd,
as desired.
Alternatively, you can note that odd powers of 4 always end in 4 (41 = 4, 43 = 64, 45 = 1024, etc.). It follows that 42k+1 + 1 ends in 5 and is therefore divisible by 5.
For yet another approach, Mir and Hecquet both used the geometric sum formula for r = –4:
S = 1 + (–4) + (–4)2 + ... + (–4)2k =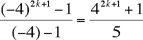 
; therefore 42k+1 + 1 = 5S so that 5 must divide evenly into 42k+1 + 1.
Proof that for n odd and greater than 3, (4n + 1)/5 cannot be a prime number.
All solutions were based on factoring 4a4 + b4. We discussed factoring fourth-degree polynomials in general (and this polynomial in particular) as part of the solution to MP41 in April 2004. Indeed,
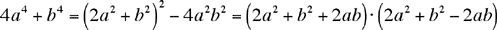
To apply this factorization to 4n + 1, we note that we can write n = 2k+1, so that
4n + 1 = 42k+1 + 1 = 4·42k + 1 = 4·24k + 1
= (2·22k +1 + 2·2k)(2·22k +1 – 2·2k).
But (2·22k +1 + 2·2k) > (2·22k +1 – 2·2k), and the smaller factor is bigger than 5, which can be seen as follows:
2·22k +1 – 2·2k = 2k+1(2k– 1) + 1 > 22(21– 1) + 1 = 5.
Thus, when n = 2k + 1 > 3, we have k > 1; this means that 4n + 1 factors into a product of two numbers that are both strictly greater than 5, so that dividing either of these numbers by 5 leaves it greater than 1. By our preliminary exercise we saw that 4n + 1 is divisible by 5. We conclude that (4n + 1)/5 itself has two integer factors that are both greater than 1. In other words, it cannot be prime.
(–1)n = (–1)2k+1 = –1 (mod 5), so that 4n +1 
0 (mod 5),