|
Solution to February 2006 Problem
The Problem:
We are given a pair of quadratic equations with integer coefficients b and c,
x2– bx + c = 0 and x2– bx – c = 0,
and call them a compatible pair if they both have integer solutions. For example,
x2– 5x + 6 = 0 has solutions 2 and 3, while
x2– 5x – 6 = 0 has solutions –1 and 6.
Of course, we can multiply b and c by d and d2 to get a related compatible pair x2– bdx ± cd2 = 0, but we are interested in pairs where b and c have no common divisor. Are there any other compatible pairs?
This month's problem is based on the article "Curious Consequences of a Miscopied Quadratic", by Jeffrey L. Poet and Donald L. Vestal, Jr. in the College Mathematics Journal, 36:4 (September 2005), pp 273-277.
We received correct solutions from
Vincent Bardoux (France) |
|
Aleksandar Ilic' (Serbia and Montenegro) |
Pierre Bornsztein (France) |
|
Wolfgang Kais (Germany) |
Sebastien Dumortier (France) |
|
Matthew Lim (internet) |
Philippe Fondanaiche (France) |
|
Patrick LoPresti (USA) |
| Xavier Hecquet (France) |
|
Juan Mir Pieras (Spain) |
| Karim Iaaouini (Morocco) |
|
Mark Pilloff (USA) |
| Wilfrid Pillard (France) |
|
|
Solution.
Most solvers, namely Bardoux, Bornsztein, Iaaouini, Ilic', Kais, Lim, LoPresti, and Mir, noticed the connection between compatible pairs and Pythagorean triples (which is a triple A, B, C of integers that satisfy A2 + B2 = C2). In explaining what this means, we will combine ideas from each of our correspondents.
The solution to x2– bx + c = 0 is 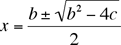 . Note that for integers b and c, b2– 4c has the same parity as b; thus if . Note that for integers b and c, b2– 4c has the same parity as b; thus if 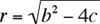 is an integer, it will also have the same parity as b, and therefore x will be an integer. The converse is immediate: if x is an integer, then so is is an integer, it will also have the same parity as b, and therefore x will be an integer. The converse is immediate: if x is an integer, then so is 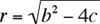 . Similarly, x2 – bx – c = 0 has integer solutions if and only if . Similarly, x2 – bx – c = 0 has integer solutions if and only if 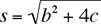 is an integer. It follows that is an integer. It follows that
b and c determine a compatible pair if and only if there exist integers r and s that satisfy
r2 = b2– 4c and s2 = b2 + 4c.
Theorem. Define 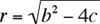 and 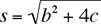 . If b and c determine a primitive compatible pair then 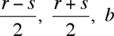 is a primitive Pythagorean triple; conversely, if A, B, C is a primitive Pythagorean triple, then r = A – B and s = A + B lead to a primitive compatible pair whose coefficients satisfy 2 b2 = r2+ s2 = 2( A2 + B2) and 8 c = s2– r2 = 4 AB.
Proof. Assume that b and c form a primitive compatible pair. The definitions give
(r – s)2/4 + (r + s)2/4 = (1/4)(r2– 2rs + s2 + r2 + 2rs + s2)
= (1/2)(r2 + s2) = (1/2)(b2– 4c + b2 + 4c) = b2,
so that 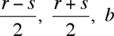 is a Pythagorean triple. We simply have to check that the three integers are relatively prime when b and c are. If d > 1 divides the first two, then d2 would divide their product (r2– s2)/4 = 2c, so that d would divide c. Since we assume the pair b, c to have no divisor except 1, then no nontrivial divisor of c would divide b; consequently the triple will have no common divisor except 1. is a Pythagorean triple. We simply have to check that the three integers are relatively prime when b and c are. If d > 1 divides the first two, then d2 would divide their product (r2– s2)/4 = 2c, so that d would divide c. Since we assume the pair b, c to have no divisor except 1, then no nontrivial divisor of c would divide b; consequently the triple will have no common divisor except 1.
For the converse, we start with the Pythagorean triple A, B, and C = 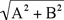 = b. Then A and B cannot both be odd (because squares of integers can be only 1 or 0 modulo 4), so that c = AB/2 is also an integer. We check easily that = b. Then A and B cannot both be odd (because squares of integers can be only 1 or 0 modulo 4), so that c = AB/2 is also an integer. We check easily that 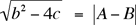 and and 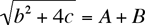 are both integers, so these serve as the numbers r and s that correspond to the pair b and c (as we saw before the statement of the theorem). Moreover, any prime divisor of both b and c would necessarily divide C (= b) and at least one of A or B; therefore (since A2 + B2 = C2) it would necessarily divide all three of A, B, and C, so that the Pythagorean triple we began with would not be primitive. In other words, if the triple is primitive, then so is the corresponding compatible pair b and c. are both integers, so these serve as the numbers r and s that correspond to the pair b and c (as we saw before the statement of the theorem). Moreover, any prime divisor of both b and c would necessarily divide C (= b) and at least one of A or B; therefore (since A2 + B2 = C2) it would necessarily divide all three of A, B, and C, so that the Pythagorean triple we began with would not be primitive. In other words, if the triple is primitive, then so is the corresponding compatible pair b and c.
Books on elementary number theory tell us that we can generate all primitive Pythagorean triples by starting with any two integers m and n that satisfy
m > n; m and n have different parity and no common divisor except 1.
By putting all the pieces together we can build all pairs b and c from m and n and an arbitrary positive integer k:
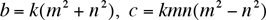 , ,
and for these b and c, the solutions to x2 – bx + c = 0 are x =
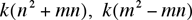 , ,
and the solutions to x2 – bx – c = 0 are x =
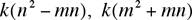 . .
The resulting compatible pairs are primitive if and only if k = 1.
Here are the first few examples of primitive compatible pairs.
m |
n |
b |
c |
Compatible pairs |
2 |
1 |
5 |
6 |
x2– 5x + 6 = (x – 3)(x – 2)
x2– 5x – 6 = (x – 6)(x + 1) |
3 |
2 |
13 |
30 |
x2– 13x + 30 = (x – 10)(x – 3)
x2– 13x – 30 = (x – 15)(x + 2) |
4 |
1 |
17 |
60 |
x2– 17x + 60 = (x – 5)(x – 12)
x2– 17x – 60 = (x – 20)(x + 3) |
4 |
3 |
25 |
84 |
x2– 25x + 84 = (x – 4)(x – 21)
x2– 25x – 84 = (x – 28)(x + 3) |
Poet and Vestal's main result in their CMJ article was a theorem very much like ours. They went on to interpret familiar facts about Pythagorean triples as statements about compatible pairs. For example, if b has a prime factor congruent to 1 modulo 4, then there is a compatible pair x2 – bx ± c. Furthermore, if the prime factorization of b contains only primes congruent to 1 modulo 4, then the corresponding compatible pair is primitive. Further questions are discussed on Vestal's web page http://staff.missouriwestern.edu/~vestal/talks.html.
There are other nice ways to approach our problem. Hecquet and Pilloff simplified their work by providing a one-parameter family of primitive compatible pairs, namely
b = n2 + (n + 1)2,
c = n(n + 1)(2n + 1).
Fondanaiche also began with the equations r2 = b2– 4c and s2 = b2 + 4c, and added them to get 2b2 = r2 + s2. He interpreted this as a family of Pell equations and used that theory to produce primitive compatible pairs. For example, if you set s = 1, and start with the solution r = 7, b = 5 (and c = (r2 – 1)/8 = 6), you obtain a one-parameter family by defining the column vector X1 = 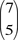 , and using the recursion Xn = , and using the recursion Xn = 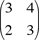 Xn–1. For the case s = 1 the solutions to the resulting Pell equation 2b2 = r2 + 1 are Xn–1. For the case s = 1 the solutions to the resulting Pell equation 2b2 = r2 + 1 are
r |
b |
c |
7 |
5 |
6 |
41 |
29 |
210 |
239 |
169 |
7140 |
1393 |
985 |
242556 |
... |
... |
... |
Dumortier kindly supplied a computer printout of all primitive compatible pairs b, c having c < 1000:
5, 6
13, 30
17, 60
25, 84
29, 210
37, 210
41, 180
53, 630
61, 330
65, 504
65, 924
85, 546
101, 990
113, 840.
|

