|
Solution to May 2006 Problem
The Problem:
Find the greatest common divisor of the 1003 integers
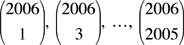
where 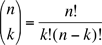 is the number collections of k objects that can be formed from a set of n objects. is the number collections of k objects that can be formed from a set of n objects.
We received correct solutions from
Saïd Amghibech (Québec) |
|
Xavier Hecquet (France) |
Pierre Bornsztein (France) |
|
Wolfgang Kais (Germany) |
| John Campbell (Alberta) |
|
Matthew Lim (USA) |
| Saturnino Campo Ruiz (Spain) |
|
Patrick LoPresti (USA) |
| Jean-Denis Eiden (France) |
|
Juan Mir Pieras (Spain) |
| Federico Felizzi (Berlin) |
|
Joseph Najnudel (France) |
| Philippe Fondanaiche (France) |
|
Mark Pilloff (USA) |
| H.N. Gupta (Regina) |
|
|
Solution.
Let D be the greatest common divisor that we seek. We shall see that D = 2.
Step 1. D divides 22005.
From the binomial formula,
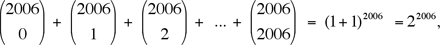
and
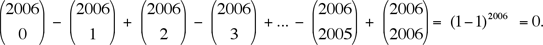
By subtracting the second from the first then dividing by 2, we get
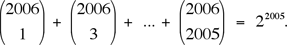
Therefore, the greatest common divisor D of 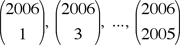 must divide their sum 22005, as claimed. must divide their sum 22005, as claimed.
Step 2. Since D also must divide 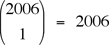 = 2·1003, we see that = 2·1003, we see that
D is either 1 or 2.
Step 3. 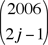 is even for j = 1, ..., 1003. is even for j = 1, ..., 1003.
We use the identity (discussed below) 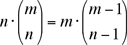 to find that to find that
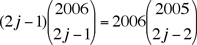 . .
Since the right side is an even integer while 2j – 1 is always odd, we deduce that 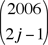 must be even. That is, all our binomial coefficients are even. must be even. That is, all our binomial coefficients are even.
We conclude that D = 2, as claimed.
Comments and generalizations.
Step 3 depends on a familiar identity. You can verify it, if you wish, by doing the arithmetic:
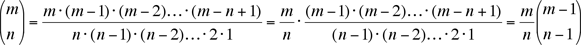
or, you can use a "committee argument":
To select an n-member committee with a chairman you can either pick the n members (in one of  ways) and choose the chairman from among them, or you can first select the chairman from the entire group of m and then choose the remaining n – 1 members of the committee from the remaining m-1 members of the group. ways) and choose the chairman from among them, or you can first select the chairman from the entire group of m and then choose the remaining n – 1 members of the committee from the remaining m-1 members of the group.
In place of step 1, five of our correspondents made direct use of the fact that
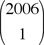 = 2006 = 2·17·59, which implies that D divides 2·17·59. They simply had to show that = 2006 = 2·17·59, which implies that D divides 2·17·59. They simply had to show that 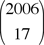 is not divisible by 17 while is not divisible by 17 while 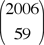 is not divisible by 59. One advantage to our featured argument is that our same three steps show, more generally, that is not divisible by 59. One advantage to our featured argument is that our same three steps show, more generally, that
For q odd, the greatest common divisor of 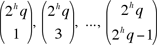 is 2h. is 2h.
We thank Gupta, Mir, and Campo for this observation. Matthew Lim took the generalization even farther. He proved that
If p is a prime number and m is a fixed integer that is relatively prime to p, then ph is the greatest common divisor of numbers of the form 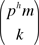 , with 1 ≤ k < phm and k relatively prime to p. , with 1 ≤ k < phm and k relatively prime to p.
For him, step 1 had to be replaced by an
argument that if q is a prime divisor of m and qb is the largest power of q that divides m, then q does not divide 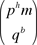 . The details are not difficult, particularly if you know a useful theorem of Kummer. We discussed these ideas and provided references in our solution to the problem of June, 2001. . The details are not difficult, particularly if you know a useful theorem of Kummer. We discussed these ideas and provided references in our solution to the problem of June, 2001.
| 
