|
Solution to January 2006 Problem
Greetings for the new year. The Monthly Problem team wishes you all the health and happiness this coming year as you enjoyed last year.
The Problem:
Find the maximum value of f(2006) - f(2005) where f is a real valued function that satisfies the inequality
|f(x) - f(y)| ≤ (x-y)2
for all real numbers x and y.
We received correct solutions from
Saïd Amghibech (Québec) |
|
Aleksandar Ilic (Serbia and Montenegro) |
Vincent Bardoux (France) |
|
Wolfgang Kais (Germany) |
Pierre Bornsztein (France) |
|
Normand Laliberté (Ontario) |
Sebastien Dumortier (France) |
|
Matthew Lim (internet) |
| Philippe Fondanaiche (France) |
|
Juan Mir Pieras (Spain) |
| Xavier Hecquet (France) |
|
Mark Pilloff (USA) |
Solution.
It turns out that f is a constant function so that f(x) = f(y) for all values of x and y; in particular,
f(2006) – f(2005) = 0.
Our contributors provided two ways of seeing this.
Method 1. (We use the triangle inequality.)
Let n be a positive integer and define xk = 2005 + k/n for k = 0, 1, ..., n. Then
|f(2006) – f(2005)|= |f(xn) – f(x0)|
= |(f(x1) – f(x0)) + (f(x2) – f(x1)) +... + (f(xn) – f(xn–1))|
≤ |(f(x1) – f(x0))| + |(f(x2) – f(x1))| +... + |(f(xn) – f(xn–1))|
(by the triangle inequality)
≤ (x1– x0)2 + (x2– x1)2+... + (xn– xn–1)2 (by the definition of f)
= n(1/n)2 (by the definition of xk)
= 1/n
Since |f(2006) – f(2005)| ≤ 1/n for all positive integers n, f(2006) – f(2005) = 0 as claimed. Of course, in the above argument we can replace 2006 by x, 2005 by y, and let xk = x + k(y – x)/n, thereby proving that f(x) – f(y) = 0 for all x and y. In other words, f is constant.
Method 2. (We use basic calculus.)
When we set y = x + h, the given inequality becomes
|f(x + h) - f(x)| ≤ (x + h – x)2 = h2.
Thus, for fixed x and for all h,
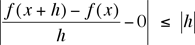 . .
Letting h go to zero we see that the limit of the quotient is zero. Thus, f is differentiable for all x and its derivative satisfies f '(x) = 0, which implies that f(x) is constant. Thus, we again see that f(x) = f(y) for all x and y.
| 
