|
Solution for March 2009
| The Problem: |
 |
MP84 March 2009
A polyhedron with six edges is called a tetrahedron, and a polyhedron with eight edges is called a quadrangular pyramid. What is a polyhedron with seven edges called?
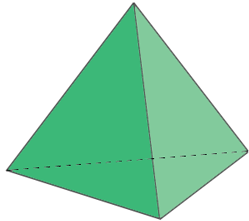
Tetrahedron
6 edges |
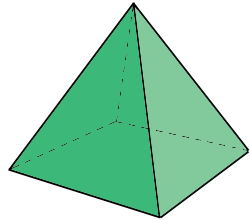
Quadrangular Pyramid
8 edges |
Background. For our purposes, a polyhedron is a solid figure bounded by polygonal faces. Each of its edges joins two vertices and is a common side of two adjacent faces. A vertex is a point where three or more edges meet, and it forms a corner where three or more faces come together.
|
Correct responses: |
|
Correct solutions were sent in this month by
Bojan Basic (Serbia) |
Cornel Gruian (Romania) |
Luigi Bernardini (Italy) |
Omran Kouba (Syria) |
Gérard Billion (France) |
Catherine Nadault (France) |
Lou Cairoli (USA) |
John T. Robinson (USA) |
Olivier Cyr (France) |
Albert Stadler (Switzerland) |
Sébastien Dumortier (France) |
A. Teitelman (Israel) |
Philippe Fondanaiche (France) |
Karim Laaouini (Morocco) |
|
The solution:
Answer. A seven-edged polyhedron is called nonexistent: no polyhedron can have exactly seven edges! Evidently this is a "well-known" result: Robinson found two web pages that discuss it:
http://www.maths.usyd.edu.au/u/sandrab/math2009/t06sol.pdf (see point 5 there), and
http://plus.maths.org/issue43/features/kirk/proof.html.
You can google "polyhedron seven edges" for further references. Our correspondents produced a variety of arguments; we shall feature three of them, and then show that the number of edges of a polyhedron can take any value greater than seven.
Notation. For a given polyhedron we shall denote by v the number of its vertices, f the number of its faces, and e the number of its edges. Euler's theorem for convex polyhedra (which means, roughly speaking, that their faces can be drawn on the surface of a sphere)says that these quantities are related by
v – e + f = 2
For example, for a tetrahedron v = 4, f = 4, and e = 6. Our first two methods avoid appealing to Euler's theorem.
Method 1 (the approach of Billion and Dumortier).
Each edge joins two vertices while each vertex is the end of at least three edges; therefore,
3v ≤ 2e.
Since we want e = 7, we must have v ≤ 14/3, so that v (an integer) would necessarily be 4. But 4 vertices can determine at most
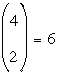
edges, which is a contradiction. We conclude that e cannot be 7.
Method 2 (the approach of Gruian, Kouba, and Robinson).
For a polyhedron to have a face with four or more vertices, it would necessarily have 8 or more edges: the face accounts for at least 4 edges while each of its vertices must be joined to a vertex which is outside the plane of that face. Since we want there to be only 7 edges, we conclude that the faces must all be triangles. Since each face then will contain exactly 3 edges while each edge belongs to two faces, we would have 3f = 2 × 7, which is not possible for an integer f.
Method 3 (the most popular approach, although restricted to convex polyhedra).
Since a polyhedron with 4 vertices can have at most
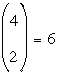edges, any 7-edged polyhedron would need at least 5 vertices. Similarly, with only 4 faces it could have at most 6 edges, whence it would need at least 5 faces. But then we would have v + f ≥ 10, contradicting Euler's theorem which, with e = 7, says that v + f = 9.
Further comments. It is clear that a polyhedron must have at least four vertices, so that it must have at least six edges. We have seen that the number of edges cannot be seven. Cairoli addressed the question of whether or not there exist other excluded values of e. The answer is easily seen to be no:
There exists a polyhedron having exactly e edges for e = 6 and for e ≥ 8.
A pyramid with a n-gonal base has e = 2n edges; thus, any even number 6 or greater is a possible value for e. Next, we can truncate this pyramid to obtain a polyhedron with an odd number of edges by cutting a tetrahedral-shaped corner off the base: the vertex at the base of the pyramid is replaced by a triangular face, leaving a polyhedron with e = 2n + 3 edges, whence any odd number 9 or greater is a possible value for e. Alternatively, place a tetrahedral cap on one of the triangular faces of the pyramid. That adds 3 more edges, again making a total of e = 2n + 3 edges. (For those who worry about the convexity of the polyhedron that results from this last procedure, when the base of the pyramid has more than 4 vertices, the vertex of the cap can be taken inside the tetrahedron formed by extending the planes of the base and of two faces adjacent to the same triangular face of the pyramid.)
|
