|
Solution for May 2009
| The Problem: |
 |
MP87 May 2009
Our goal this month is to correct a flaw in the usual ordering of the positive integers: when n is odd then it divides 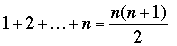 but when n is even then it does not divide 1 + 2 + ... + n; so it is only half the time that the nth integer divides the sum of all the integers up to it. Our problem is to find a better ordering of the positive integers; specifically, but when n is even then it does not divide 1 + 2 + ... + n; so it is only half the time that the nth integer divides the sum of all the integers up to it. Our problem is to find a better ordering of the positive integers; specifically,
find a sequence a1, a2, a3, ... of positive integers such that
(i) every positive integer appears exactly once in the sequence, and
(ii) for every n, an divides a1 + a2 + ... + an.
|
Correct responses: |
 |
Correct solutions were sent in this month by
Philippe Fondanaiche (France)
|
John T. Robinson (USA) |
|
Patrick J. LoPresti (USA) |
Albert Stadler (Switzerland) |
|
The solution:
Our solution includes ideas from all
correspondents. Obviously we cannot start with a1 =
1, because there is no suitable choice for a2. So
we start with a1 = 2, and follow the following
strategy:
Strategy 1: If a1,
a2, ..., an are
already selected, we put sn
= a1 + a2 + ... + an,
and select an+1 as the smallest divisor of sn not yet chosen.
n:
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
an:
|
2
|
1
|
3
|
6
|
4
|
8
|
12
|
9
|
5
|
10
|
15
|
25
|
20
|
24
|
16
|
sn:
|
2
|
3
|
6
|
12
|
16
|
24
|
36
|
45
|
50
|
60
|
75
|
100
|
120
|
144
|
160
|
The first few values of an are
shown in the table above. For n
> 1 we have sn >
a1, a2, ..., an, hence it is always possible to select a next value an+1,
which will be at most sn.
It is clear that this infinite sequence satisfies property (ii), but
not so clear that it also satisfies property (i). In fact our
correspondents looked up this sequence in the Online Encyclopedia of
Integer Sequences http://www.research.att.com/~njas/sequences/,
where it is conjectured that this sequence contains all the positive
integers. Since we cannot prove the conjecture, after a while we
abandon Strategy 1 and switch to:
Strategy 2:
Suppose a1, a2, ..., an
are already chosen and we start to worry because some integer N has not yet appeared. If sn is a power of 2, we
use Strategy 1 for one more step to get a sum which is not a power of
2. Then we start appending terms ak+1
= sk until we are sure to reach a multiple of N by appending suitable powers of 2.
The first step is to dispose of the undesirable
situation when sn = 2k.
In this case we cannot have all the previous powers of 2 already used,
for otherwise we would have
sn - 1 = 1 + 2 + ... + 2k-1
< a1 + ... + an = sn,
and the only way to complete the sequence would be to
have n = k+1 and a second term equal to 1.
Hence Strategy 1 yields a new term 2i
with i < k, and the next sum 2k + 2i is not a power of two.
Therefore without loss of generality we may assume that
we start worrying about N at
a point when sn is
not a power of 2. We can also assume that N is odd because of the following argument. We put an+1
= sn
whence sn+1 = 2sn,
then an+2
= 2sn whence sn+2 = 4sn,
and we keep appending terms of the form an+j = 2j-1sn
to get sn+j = 2jsn, until 2j is large
enough. To understand what we mean by ``large enough'', we will examine
the sequence of powers of 2 modulo N.
For every integer i,
let bi be the
remainder of division of 2i
by N. Since there are only
finitely many remainders to chose from, there exist integers i, k such that bi+k = bi. We then have bi+k+1 = bi+1, bi+k+2 = bi+2, and the
sequence keeps cycling through the terms bi, bi+1, ...,bi+k-1. Note that bi +
bi+1 + ... + bi+k-1
≡ 0 (mod N). Indeed for t = bi +
bi+1 + ... + bi+k-1, we get
2 t = 2 bi +
2bi+1 + ... + 2bi+k-1
≡ bi+1 +
bi+2 + ... + bi ≡ t (mod N)
whence t
≡ 0 (mod N).
Now sn admits a
representation as a sum of distinct powers of 2, whence for any j > i, 2 jsn is
congruent modulo N to a sum
of terms in bi, bi+1, ..., bi+k-1. With the
identity 2 bm
≡ bm+1
(mod N), we can simplify the
sum until we get a sum of distinct terms in bi, bi+1, ..., bi+k-1 which is
congruent modulo N to 2 jsn. Let bm(1), ..., bm(r) be the terms in bi, bi+1, ..., bi+k-1 which are not
used in this sum. If we picked j
large enough, we can pick a decreasing sequence 2 j
> 2 e(1)
> ... > 2 e(r)
such that 2 e(p)
≡ bm(p) (mod N), 2 e(1),
..., 2 e(r) do not
appear in the sequence a1, a2, ..., an.
Since sn is
not a power of 2, 2 e(1),
..., 2 e(r) do not
appear either in the remaining terms an+1
= sn,
..., an+j = 2 j-1sn.
Therefore we can pick an+j+1
= 2 e(1) , sn+j+1 = 2 e(2)q1, an+j+2 = 2 e(2) , sn+j+1 = 2 e(3)q2, ...,
up to an+j+r = 2 e(r). We then have
sn+j+r = 2jsn + 2e(1) + ... + 2e(r) ≡
0 (mod N).
Thus we can select an+j+r+1 = N.
Here is how the process works up to n = 12. We begin with Strategy 1,
|
n |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
an |
2 |
1 |
3 |
6 |
4 |
|
|
|
|
|
|
sn |
2 |
3 |
6 |
12 |
16 |
|
|
|
|
|
|
which gets us a sequence of length 5 with numbers up to 4. We now want N = 5 in our sequence. Because s5= 16 is a power of 2, we take a6= 8 so that s6= 24. We will be working mod 5 (because N = 5), which means that we might need as many as N – 1 = 4 powers of 2 that exceed 8 (the largest power of 2 that has thus far appeared); that is, we might need
b4= 24 = 16 ≡ 1 (mod 5),
b5 = 25 = 32 ≡ 2 (mod 5),
b6 = 26 = 64 ≡ 4 (mod 5),
b7 = 27 = 128 ≡ 3 (mod 5).
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
an |
2 |
1 |
3 |
6 |
4 |
8 |
24 |
48 |
96 |
32 |
16 |
5 |
... |
sn |
2 |
3 |
6 |
12 |
16 |
24 |
48 |
96 |
192 |
224 |
240 |
245 |
|
We use an = sn–1 up to sn–1 = 192 = 64·3: at s6= 24 ≡ 4 (mod 5) we need a7 ≡ 1 (mod 5) for the next term, but we cannot use a7= 16 because it does not divide 24; similarly with s7= 48 ≡ 3 (mod 5) we need a8 ≡ 2 (mod 5), but 32 does not divide 48, and with s8= 96 ≡ 1 (mod 5) we need a9 ≡ 4 (mod 5), but 64 does not divide 24. Finally, with s9= 192 ≡ 2 (mod 5) we need a10 ≡ 3 (mod 5), and although 128 does not divide 192, we can now use 32 + 16 ≡ 3 (mod 5) and save 64 and 128 for a future step. Consequently we set a10= 32 and a11= 16, which allows us to set a12 = 5, as promised. The next missing number is N = 7, so we will possibly use the next N – 1 = 6 powers of 2 (starting with 64), and the process continues ad infinitum.
A related problem.
Fondanaiche reported that he came across a problem from the 12th Nordic Mathematical Contest (1998) that is closely related to our problem. It asked for a rearrangement an of the positive integers in which the partial sums sn = a1 + ... + an are divisible by n (unlike our problem where sn is divisible by an). Patrick LoPresti, Lou Cairoli, Ruben Victor Cohen, and Bojan Basic also sent in solutions to this variation of the problem. Here is a composite of their similar solutions.
Define the arrangement recursively: Let a1 = 1, and set
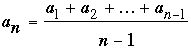
if this number is not already in the sequence; otherwise set
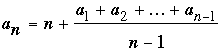
Note that in the first case
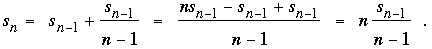
In the second case,
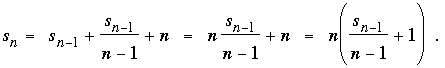
In both cases we see that sn is divisible by n, as desired. Moreover, the difference between successive quotients 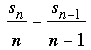 is either 0 or 1. The sequence of quotients grows monotonically without bound (since the difference cannot be 0 twice in a row). Since an is defined to be equal to the value of the quotient if that value has not yet appeared, every positive integer must eventually be reached. On the other hand, because the quotients are increasing it is not possible that is either 0 or 1. The sequence of quotients grows monotonically without bound (since the difference cannot be 0 twice in a row). Since an is defined to be equal to the value of the quotient if that value has not yet appeared, every positive integer must eventually be reached. On the other hand, because the quotients are increasing it is not possible that 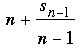 can equal a previous can equal a previous 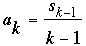 or or 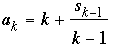 for k < n. Here, then, are the first 14 terms of the resulting sequence. for k < n. Here, then, are the first 14 terms of the resulting sequence.
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
an |
1 |
3 |
2 |
6 |
8 |
4 |
11 |
5 |
14 |
16 |
7 |
19 |
21 |
9 |
|
sn |
1 |
4 |
6 |
12 |
20 |
24 |
35 |
40 |
54 |
70 |
77 |
96 |
117 |
126 |
... |
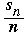
|
1 |
2 |
2 |
3 |
4 |
4 |
5 |
5 |
6 |
7 |
7 |
8 |
9 |
9 |
|
|

