|
Solution for December 2008
| The Problem: |
 |
MP82 December 2008
A point is placed inside an equilateral triangle so that its distances from the three vertices are 5, 12, and 13. Find the area of the triangle.
|
Correct responses: |
 |
Complete solutions were submitted to us by
Bernard Collignon (France) |
Shpetim Rexhepi (Macedonia) |
Ivan Hoffmann de Visme (UK) |
John T. Robinson (USA) |
Philippe Fondanaiche (France) |
K. Sengupta (India) |
Patrick J. LoPresti (USA) |
Albert Stadler (Switzerland) |
Catherine Nadault (France) |
A. Teitelman (Israel) |
Lou Cairoli (USA) |
Mark Pilloff (USA) |
| Daniel Y. Lu (?) |
Daniel Nix (Australia) |
| Luigi Bernardini (Italy) |
Jose Arraiz (Brazil) |
| Bojan Basic (Serbia) |
Matthew Lim (USA) |
| Gerard Billion (France) |
John Dukellis (Boeing = USA?) |
| Baptiste Gorin (France) |
|
In addition, both Farid Alberto Lian Martínez (Colombia) and Jason Ganley provided numerical solutions. Our complete solutions exploited four different methods. The problem has been around for a long time; after we show our four solutions we will discuss some references we managed to locate.
|
The solution:
Solution 1. Our solution combines ideas from Fondanaiche, LoPresti, Rexhepi, Robinson, and Sengupta.
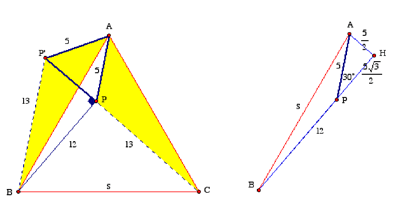
FIGURE 1
In Figure 1, ΔABC has sides of length s and an interior point P. A
clockwise rotation through 60° about A takes C to B and P to a point P'; thus AP' = AP = 5, BP'
= 13, and (because ΔAP'P is
equilateral), P'P = 5. It
follows that ΔBP'P has
sides 5, 12, and 13, whence the angle at P is 90°. Consequently, ∠BPA = 60° + 90° =
150°. The cosine law (with cos 150° =
–√3/2) then says that s satisfies
s2 = AB2 = 52 + 122 –
2·5·12cos 150° = 169 + 60√3.
The area of ΔABC is therefore
which equals about 118.18.
Fondanaiche
avoided using the cosine law in his solution by extending BP to the foot of the perpendicular from A, called H in the above diagram on the right. ΔAPH is then a right triangle with angles of 30° and
60°,
so that AH = 5/2 and PH = (5√3)/2, whence
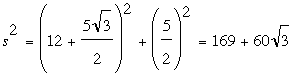
as before.
2 Collignon's Solution.
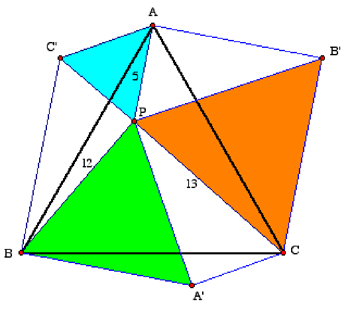
FIGURE 2
For this solution we rotate P
clockwise through 60° about A to get C', about B to get A', and about C to get B'. We note that ΔAC'B is congruent to ΔAPC, ΔBA'C is congruent to ΔBPA,
and ΔCB'A is congruent toΔCPB; this tells us that the area of the hexagon AC'BA'CB' is exactly twice the area [ABC] that we seek. We see that the hexagon consists of three equilateral triangles (whose
equal sides have length 5, 12, and 13), and three congruent right
triangles. Thus,
2[ABC] = [AC'BA'CB']
=
[AC'P] + [BA'P] + [CB'P]
+ 3[PC'B]
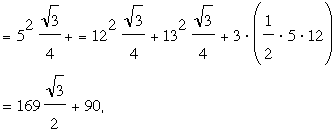
and [ABC] =
169(√3/4) + 45.
3 Nadauld's Solution.
Instead of rotating the point P, we reflect it in the sides AB to get C', BC to get A', and CA to get B'. Because each triangle inside ΔABC that shares the vertex P (such as
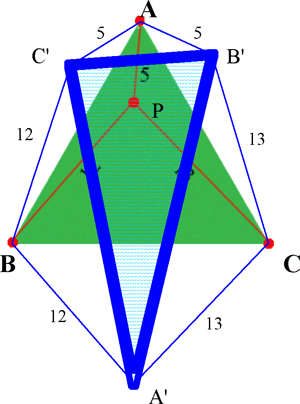
FIGURE 3
ΔAPB) is
congruent to its reflected image (namely ΔAC'B), the area [AC'BA'CB'] of the outside hexagon is twice the area [ABC] of the given triangle. Each of the triangles AC'B', BA'C', CB'A' are isosceles with an apex angle of 120°;
indeed, each is composed of a pair of 30-60 right triangles with respective
hypotenuses 5, 12, and 13. The
sides opposite the 120° angles therefore have lengths B'C' = 5√3, C'A' =
12√3, and A'B' = 13√3, which
implies that ∠A'C'B' = 90°. Consequently,
2[ABC] = [AC'BA'CB']
=
[AC'B'] + [BA'C'] + [CB'A']
+ [A'B'C']
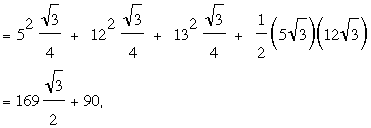
and [ABC] =
169(√3/4) + 45.
Solution 4. A
version of this solution came from de Visme, Stadler, and Teitelman. We present Stadler's solution.
Let α, β, and γ be the three angles at P; specifically let α = BPC, β = ∠CPA, and γ = ∠APB. Let s be the side of the triangle. Then, by the Law
of Cosines:
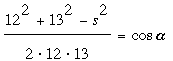 , , 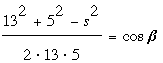
and 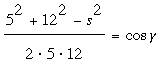 (*) (*)
Because α + β + γ = 2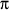 , we have , we have 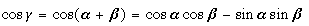 ; whence ; whence 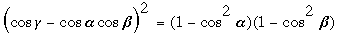 , and finally, , and finally,
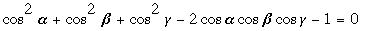
We insert
the values from (*) into this equation and get a sixth degree equation for the
side s, namely
s2(s4 - 338 s2 + 17761) = 0.
(A computer
algebra system is helpful in this last step!) This last equation has the solutions s2 =0, and s2 = 169 ± 60√3. A quick check
exhibits that only the solution s2 = 169 + 60√3 satisfies α + β + γ = 2 . This value of s2 produces the value . This value of s2 produces the value
[ABC] =
169(√3/4) + 45 for the area of the triangle.
Comments. Several correspondents noted that
there is nothing special about a 5-12-13 right triangle. The same four arguments would produce
the area of ΔABC any time the distances a, b, and c to the vertices from P satisfy a2 + b2 = c2. Robinson further generalized the
problem; he found the area [ABC] for any point P inside the triangle in terms of the distances a = PA, b = PB, and c = PC. In fact, our solution 3 (from Nadauld) gives us the answer with no
further work: instead of finding the area of ΔA'B'C' by using properties of right triangles, we can
use Heron's formula and obtain,
[ABC] = ½ [AC'BA'CB']
= ½ ([AC'B'] + [BA'C'] + [CB'A']
+ [A'B'C'])
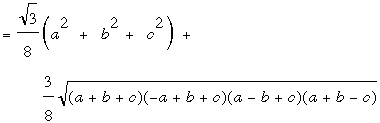
A remarkable consequence of this argument is that no matter
where P is chosen inside the equilateral
triangle, the distances a, b, c satisfy the triangle inequality; in other words, the distances from P to the vertices are not arbitrary, but must form the
sides of ΔA'B'C'. Dimitrie Pompeïu made this observation in 1936. In fact, Pompeïu's Theorem states that'
For any point P in the plane of DABC, the lengths of the line segments PA, PB, PC correspond to the
sides of a triangle except when P lies on the circumcircle of ΔABC, in which case the reflections of P in the sides, namely A', B', C', would lie on a line.
Sengupta
pointed us to the MathWorld web page
http://mathworld.wolfram.com/EquilateralTriangle.html
where there is a neat formula from Martin Gardner (Mathematical
Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American, New York: Vintage Books, 1977, pages 56-57 and 63)
for the side s of the equilateral
triangle:
3(a4 + b4 + c4 + s4)=(a2 + b2 + c2 + s2 )2 ;
this equation can be obtained by replacing [ABC] with s2√3/4
in Robinson's equation just above, then rearranging terms. Richard Guy reports (in Unsolved
Problems in Number Theory, 2nd ed. New
York: Springer-Verlag, 1994; see especially Section D19, page 183) that a
computer search showed that a =
57, b = 65, c = 73, and s = 112 is the smallest example for which all the parameters are
integers. Moreover, there is an
infinite family of integer solutions given by
a = m2 + n2, b = m2 + mn + n2, c = m2 – mn + n2,
with m = 2(u2 + v2), n = u2 + 4uv + v2
and, therefore,
s = 8(u2 – v2)(u2 + uv + v2).
Our own modest search found the
problem discussed at least twice by Dr. Math:
http://mathforum.org/library/drmath/view/61863.html,
whose source was a Mensa problem
around 2002, and item 55022 where there is a discussion from 1998. It can also be found as problem 3682 in School Science and Mathematics around
1975 (according to Stanley Rabinowitz's Index to Math Problems 1975-1979, p. 135). See also Charles W. Trigg, Mathematical Quickies: 270 Stimulating Problems with Solutions. Dover (1985); originally published in 1967.
|

