Solution for April 2009

The Problem:
	MP85 April 2009 Find integers a and b such that neither 7 nor 18 divides ab(a+b), while 77 does divide (a+b)7-a7-b7.

Correct responses:

Correct solutions were sent in this month by Bojan Basic (Serbia) Tarik Kaced (France) Ruban Victor Cohen (Argentina) Omran Kouba (Syria) Bernard Collignon (France) Matthew Lim (USA) Allen Druze (USA) Benjamin Louradour (France) Sébastien Dumortier (France) Pavan Manjunath (India) Philippe Fondanaiche (France) John T. Robinson (USA) Cornel Gruian (Romania) Albert Stadler (Switzerland) Edward Doolittle (Regina

The solution:

Our April problem was based on Problem 2 from the 25th International Mathematical Olympiad (Prague, 1984).  The original statement with a solution by Jeremy Kahn can be found in International Mathematical Olympiads 1978-1985, edited by Murray S. Klamkin (Mathematical Association of America, New Mathematical Library #31, 1986).  Most of our correspondents provided a general solution, but Doolittle, Kouba, Lim, and Robinson went further and found necessary and sufficient conditions on the integers a and b for there to exist a solution:

We provide a composite of their similar arguments after first working a few simple examples.  For an example try a = 1; then k = 0 is not allowed (because 9 divides 0), but k = 1 leads to b = 361 and k = –1 leads to b = –325.  For both these examples the quotient 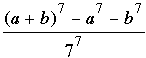is a rather large integer.  For a more tractable example take a = 20 and k = –1; then b = 17 and .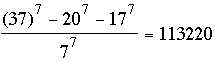

Proof of the claim.  For integers a and b we have

(a + b)⁷ – a⁷– b⁷ = 7ab(a + b)(a² + ab + b²)²,

so that (a + b)⁷ – a⁷– b⁷ is a multiple of 7⁷ precisely when ab(a + b)(a² + ab + b²)² is a multiple of 7⁶.  Moreover, since we are told that 7 does not divide ab(a + b), it follows that 7⁶ divides (a² + ab + b²)² and, therefore,

7³ divides a² + ab + b².

Because 18 × 19 = 342 = 7³ – 1, we can factor the quadratic modulo 7³ as

a² + ab + b² ≡ a² + ab + (1 – 343)b² ≡ (a + 19b)(a – 18b)
                                                 ≡ –19(18a – b)(a – 18b) ≡ 0 (mod 7³).

(For those who are not familiar with the "congruence notation", the display simply tells us that 7³ divides evenly into the product –19(18a – b)(a – 18b) and, therefore, into the product (18a – b)(a – 18b).)  Next, were 7 to divide both 18a – b and a – 18b, it would divide their difference 18a – b – (a – 18b)= 17(a + b) and, therefore, 7 would necessarily divide a + b, contradicting the assumption that 7 not divide ab(a + b).  We deduce that 7³ divides either 18a – b or a – 18b, but not both.  In the former case, should 7³ divide 18a – b then, for any integer a there exists an integer k for which b = 18a + 343k, whence the condition that 7 not divide ab(a + b) = a(18a + 343k)(19a + 343k) ≡ 6a3 (mod 7) reduces to 7 does not divide a.
            It remains to consider the further stipulation that 18 not divide ab(a + b), or (because that product is necessarily even) more simply, that 9 not divide ab(a + b).  Again letting b = 18a + 343k, we have

ab(a + b) = a(18a + 343k)(a + 18a + 343k) ≡ ak(a + k)  (mod 9),

and we deduce that 18 divides ab(a + b) if and only if 9 divides ak(a + k).  To summarize, we have determined that for the integers a and b to be solutions to our problem we must have either

b = 18a + 343k for integers a and k such that 7 does not divide a and
9 does not divide ak(a + k),
or
a = 18b + 343k for integers b and k such that 7 does not divide b and
9 does not divide bk(b + k).

Because each step was reversible, it is easy to check that our necessary conditions are also sufficient.

            Most of the submitted solutions did not factor a² + ab + b², although they did determine (as we saw above) that it must be a multiple of 7³.  Allen Druze observed that one can easily find a solution, such as a = 3, b = 6, to the much simpler problem of finding a and b such that 7 divides a² + ab + b².  Other members in this family of solutions have the form a = 3 + 7k, b = 6 + 7n, and one quickly sees a pattern that leads to finding integer pairs such as (a, b) = (–32, –29) for which 49 divides a² + ab + b²; one then uses –32 + 49k and –29 + 49n (with new k and n) to obtain finally a pair such as (17, 20) for which 343 divides 17² + 17·20 + 20².  Bojan Basic used a more systematic version of this approach based on Hensel's Lemma; he provided the Wikipedia reference
             http://en.wikipedia.org/wiki/Hensel%27s_lemma .
He observed, however, that it is much easier to type a one-line command in some computer algebra system such as Mathematica, and let it find the solutions.
            Other successful approaches involved letting the variable x represent the unknown a and treating b as a constant, then solving the congruence x² + bx + b² ≡ 0 by your favorite method, or solving the related quadratic equation

x² + bx + b² = 343k

for small integer values of k.  We know (from our detailed solution above) that such an approach will find infinitely many solutions because for any fixed b there will be many appropriate values of k.  For example, if we let b = 17 and k = 3, then x = 20 and–37, which we interpret to mean that when b = 17 we get possible solutions when a = 20 and a = –37.  It remains only to check that neither 7 nor 18 divides the resulting product
ab(a + b).