|
Solution for September 2008
| The Problem: |
 |
MP79 September 2008
The 1990 TV movie Gunsmoke: The Last Apache added an interesting twist to the traditional duel: Six shot glasses of whiskey were set on the bar; in one of them was a lethal dose of strychnine. The duelists took turns emptying the glasses with the good guy drinking first. He survived and laughed triumphantly, "Ha, you should have gone first. The first man to drink had a numerical advantage!"
Our question: What do you think about the scriptwriter's mathematical aptitude? More generally, in a duel with n glasses, with just one containing the deadly poison, the two participants take turns emptying the glasses, one at a time, until one drops dead from the poison. What is the probability that the one who drinks first is the one to die?
|
Correct responses: |
 |
Correct solutions were submitted by
Felix Arnaiz Lanzo (Spain) |
Matthew Lim (USA) |
Bojan Basic (Serbia) |
John T. Robinson (USA) |
Luigi Bernardini (Italy) |
K. Sengupta (India) |
Lou Cairoli (USA) |
Albert Stadler (Switzerland) |
Wolfgang Kais (Germany) |
Graham Ziegler (Regina) |
Farid Lian Martínez (Colombia) |
Bernard Carpentier (France) |
| Philippe Fondanaiche (France) |
|
|
The solution:
Solution. Everybody agrees that the scriptwriter got it wrong: It is a "fair" game; the probability of dying in the duel is 50% for both participants. To see this, think of the duel as a game in which each player selects three of the six glasses; the poison is arbitrarily placed in one of the six glasses, so each player has three chances out of six to drink the strychnine. A probability tree provides an alternative approach to the problem:
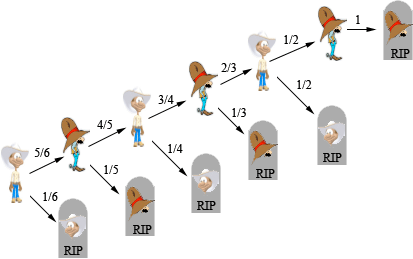
The diagram indicates that
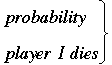 = P(dies from his 1st drink) + P(dies from 2nd) + P(dies from 3rd)
= P(dies from his 1st drink) + P(dies from 2nd) + P(dies from 3rd)
=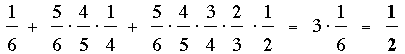 . .
Almost everybody noticed that the problem is every bit as easy should the duel be fought with n glasses to choose from, of which one contains the strychnine. When n is even each participant gets to choose exactly half of the glasses, so the probability of drinking the poison is again ½ for each. When n is odd, however, the first to drink has to select 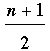 glasses, whence his probability of dying in the duel is (n+1)/2 out of n possibilities, so Probability = glasses, whence his probability of dying in the duel is (n+1)/2 out of n possibilities, so Probability =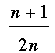 , which is always greater than ½. Kais warns that in particular, when n =1 you really should not go first. In summary, there is never an advantage to drinking first in this type of duel. It seems that the scriptwriter is now writing speeches for candidates in the current Canadian election. , which is always greater than ½. Kais warns that in particular, when n =1 you really should not go first. In summary, there is never an advantage to drinking first in this type of duel. It seems that the scriptwriter is now writing speeches for candidates in the current Canadian election.
The solution to the general problem is somewhat surprising in the following sense. If before the duel begins, one of the glasses without poison is removed, the probability that the person who drinks first dies from the first glass jumps from 1/6 (~ .167) to 1/5 (= .2), and his probability of dying in the duel increases, as one might expect, from ½ = .5 to 6/10 = .6. So, what happens if a second glass is removed? The probability that the first person to drink dies on his first drink jumps way up to ¼ = .25, but his probability of dying in the duel drops back to .5.
None of our correspondents wondered what would happen when there are n glasses, should r of them contain the poison. The formula (for the probability that the first to drink gets the poison) is not so easy to write down. The answer can be found in the article "Whisky, Marbles, and Potholes", by J. Chris Fisher and Denis Hanson, Mathematics Magazine, 68:1 (February, 1995), pages 50-54.
|

