|
Solution for February 2009
| The Problem: |
 |
MP84 February 2009
-
Find a 6-digit number that is multiplied by a factor of 6 if the final three digits are removed and placed (without changing their order) at the beginning; specifically, if we write the integer in terms of its base-10 digits as abcdef, then
6 × abcdef = defabc.
- Can you do the analogous thing with an 8-digit number? That is, can you find an 8-digit number that is multiplied by a factor of 6 when the final four digits are removed and placed (without changing their order) at the beginning?
|
Correct responses: |
 |
Correct solutions were sent in this month by
Chris Abdnour |
Omran Kouba (Syria) |
Berkay Anahtarci (Turkey) |
Normand LaLiberté (Ontario) |
Jose Arraiz (Brazil) |
Sébastien Lebre (France) |
Bojan Basic (Serbia) |
Matthew Lim (USA) |
Luigi Bernardini (Italy) |
Jeff Lindstrom (Ontario) |
Lou Cairoli (USA) |
Jean-Luc Luyet (Switzerland) |
Bernard Carpentier (France) |
Pavan Manjunan (India) |
Bernard Collignon (France) |
Daniel Nix (Australia) |
Olivier Cyr (France) |
Catherine Nadault (France) |
Philippe Fondanaiche (France) |
Shpetim Rexhepi (Macedonia) |
Baptiste Gorin (France) |
John T. Robinson (USA) |
Derek Graefer (Regina) |
K. Sengupta (India) |
Cornel Gruian (Rumania) |
Albert Stadler (Switzerland) |
| Karim Laaouini (Morocco) |
Benjamin Louradour (France) |
| Charles Huyghues Despointes (France) |
|
In addition, James Hovious sent us a computer solution, and there were three incomplete submissions. We shall first present the solution to our problem, and then discuss some generalizations. We end with a universal approach to problems that involve cyclically permuting the digits of an integer.
|
The solution:
Solution to Part (a).
We let A = abc and B = def be our pair of 3-digit integers that together form
N = abcdef. We are given that 6(1000A + B) = 1000B + A; consequently,
5999A = 994B.
The greatest common divisor of 994 and 5999 is 7, which we shall write as (994, 5999) = 7. It follows that 857A = 142B, and since (142, 857) = 1, B must be a multiple of 857. But B is a 3-digit number, whence B = 857 and, therefore, A = 142. That is, N = 142857 is the unique 6-digit number with the desired property:
6 × 142857 = 857142.
Remarks. Alternatively, one can find the prime factors of 994 and 5999, namely 994 = 2·7·71 and 5999 = 7·857. Although factoring is generally much harder than finding common factors, computer software makes the job easy for numbers that are not too big. We thank LaLiberté for pointing us to a web page that calculates prime factors:
http://www.math.wustl.edu/primes.html.
As we discuss later, many versions of our problem can be found in the problem literature. In fact Cairoli found part (a) of our problem on the Dr. Math page:
http://mathforum.org/library/drmath/view/53296.html.
Solution to Part (b).
The answer is NO, there is no such 8-digit number. Modifying the approach for part (a), we let A and B be 4-digit numbers for which 6(10000A + B) = 10000B + A; consequently,
59999A = 9994B.
Because (9994, 59999) = 1 — in fact 59999 is prime while 994 = 2·19·263 — we now deduce that B is a multiple of 59999. However, for the solution to our problem, B would necessarily be a 4-digit number. Consequently, no 8-digit number exists with the property we require.
Generalizations.
Several correspondents generalized our problem: Start with a number N whose base-10 representation has 2n digits, then split N into two parts of length n and exchange those parts (without changing the order of the digits within either part); then the resulting number equals 6N if and only if 7 divides 10n + 1 (or, equivalently, n ≡ 3 (mod 6)). Moreover, for that value of n,
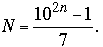
Both Fondanaiche and Stadler went a bit further and proved that no integer multiple of N (greater than 1) other than 6 will produce such a result. More precisely,
we write N = A·10n + B. The goal is to determine those positive integers A, B, n, and k for which A and B have n digits and k·(A·10n + B) = (B·10n + A); that is,
10n–1 ≤ A,B < 10n (1)
and
(10nk – 1)A = (10n – k)B . (2)
We deduce immediately from (1) and (2) that k ≤ 9. We outline Stadler's proof that if k > 1, then necessarily k = 6, n = 6j + 3, and
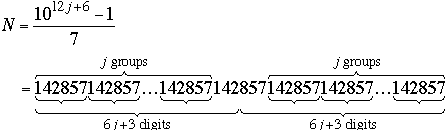
Here (as we found in the first part where j = 0 and N = 999,999 / 7 = 142857), we have
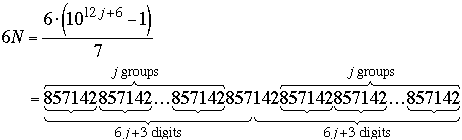
Let d = (10nk – 1, 10n – k), the greatest common divisor of the multipliers of A and B in equation (2). Note that (k –1, k + 1) is 2 or 1 according as k is odd or even. This observation allows us to deduce that
d = (10nk – 1 – k(10n – k), 10n – k) = (k2 – 1, 10n – k)
= (k – 1, 10n – k) · (k + 1, 10n – k)
= (k – 1, 10n – 1) · (k + 1, 10n + 1). (3)
We deduce easily from (3) that if k = 2, 3, 5, or 9, then d = 1. When k is 4 or 7, then
d = (3, 10n – 1) = 3. Next, consider k = 8; here 7 divides 10n – 1 if and only if n is a multiple of 6 (because 106j = (106)j ≡ 1 (mod 7)). Thus, when k = 8,
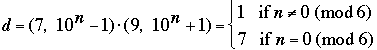
The interesting value for us is k = 6; since 1001 = 7·143, we compute that when k = 8,
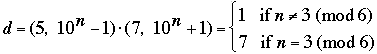
If we let g = (A, B) then (2) becomes
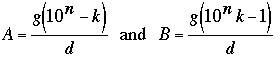
Because B must have n digits, we must have gk < d. A check of the possibilities for d discussed above shows that k < d only when k = 6, leaving us with d = 7, k = 6, g = 1, and n ≡ 3 (mod 6) for the necessary condition, as claimed.
Repeating decimals.
Although many correspondents noted the relationship of our problem in part (a) to the fraction 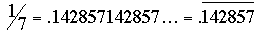 , only Matthew Lim exploited that relationship. However, not even he showed how the relationship might lead to a general method for solving a variety of related problems. Let us illustrate the idea with a very simple example: , only Matthew Lim exploited that relationship. However, not even he showed how the relationship might lead to a general method for solving a variety of related problems. Let us illustrate the idea with a very simple example:
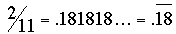 while while 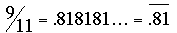
Note that 9/11 = (4.5) × 2/11, whence the problem,
Find the smallest integer which is such that if the digit on the extreme left is transferred to the extreme right, the new number so formed is four and a half times the original number.
Here we do not know how many digits to use, so we let the unknown number be
N = anan–1an–2…a2a1a0 ,
such that
9/2 N = an–1an–2…a2a1a0an .
Consider the repeating decimal
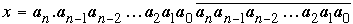
where the repeating digits are precisely those which occur in N. Now set up the obvious equations:
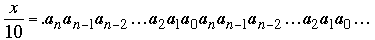
while
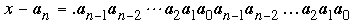
The first decimal, x/10, is a pure repeating decimal in which the digits that repeat are those in N, and the second decimal, x – an, is also a pure repeating decimal in which the digits that repeat are those in 9N/2. It follows that
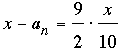
whence
11x = 20an.
For the smallest N we should take an = 1, and then x = 20/11 = .1818..., and N = 18.
The preceding discussion was based on The Gentle Art of Mathematics by Dan Pedoe (a 1973 Dover reprint of the 1959 edition published by Macmillan), pages 11-15, except that his problem used 3/2 in place of the 9/2 in our simplified version. You might want to test your favorite method against Pedoe's in his problem (with the factor 3/2) where N turns out to be the 16-digit number that forms the repeating part of 20/17.
Let us now see how Pedoe's method deals with part (a) of our February problem:
Here N = abcdef, so let x = .abcdefabcdef… and y = abc. Then
1000x – y = 6x,
whence
y = 994x = 2·7·71x.
The only value of x that yields a 3-digit value for y while at the same time is a nontrivial repeating decimal is x = 1/7. Thus x = .142857142857…, and N = 142857.
If you would like more practice, try replacing 6 in part (a) of our February problem by 5.5: Find a 6-digit number that is multiplied by a factor of 5.5 if the final three digits are removed and placed (without changing their order) at the beginning.
|

