|
Solution for November 2008
| The Problem: |
 |
MP81 November 2008
For which k ≥ 3 is a 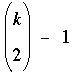 prime power pn? prime power pn?
|
Correct responses: |
 |
Our problem is Problem 984 in Crux Mathematicorum with Mathematical Mayhem, 12:1 (January 1986), pages 15-16 (in the days when the journal was just Crux Math). Solutions were submitted to us by
Bojan Basic (Serbia) |
Farid Alberto Lian Martínez (Colombia) |
Gérad Billion (France) |
Matthew Lim (USA) |
Jean Braconnier (France) |
Sébastien Racanière (UK) |
Olivier Cyr (France) |
John T. Robinson (USA) |
Dan Dima (Romania) |
Albert Stadler (Switzerland) |
Philippe Fondanaiche (France) |
Bernard Carpentier (France) |
| Catherine-A. Nadault (France) |
|
however two of our correspondents were a bit careless this month and overlooked a couple possibilities, so their solutions were incomplete.
|
The solution:
Solution. k can take the values 3, 4, 5, or 8. All of the submitted solutions came down to a similar argument. Let 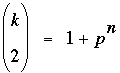 where k and n are positive integers, p prime. Then we are given where k and n are positive integers, p prime. Then we are given
(k – 2)(k + 1) = 2pn, (1)
so that either (i) k – 2 is even or (ii) k + 1 is even.
Case (i). Let k – 2 = 2m, m ≥ 1. Then (1) becomes m(2m + 3) = pn, which implies m = pr and
2pr + 3 = pn–r. (2)
- r = 0. By (2) we have m = 1 and 2m + 3 = 5 = pn; thus, k = 4, pn = 5.
- r ≥ 1. Now p must divide both sides of (2), whence p divides 3 and, therefore, p = 3. Equation (2) is then 2·3r + 3 = 3n–r, from which we get 2·3r–1 + 1 = 3n-r–1. The right-hand side cannot be 1 (because that would imply 2·3r–1 = 0); thus r – 1 = 0 (otherwise the left-hand side would be
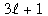 for some nonzero integer for some nonzero integer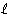 , which would not be divisible by 3). We conclude that n = 3, m = 3, and 2m + 3 = 9, implying for this subcase that k = 8, pn = 27. , which would not be divisible by 3). We conclude that n = 3, m = 3, and 2m + 3 = 9, implying for this subcase that k = 8, pn = 27.
Case (ii). Let k + 1 = 2m, m > 1. Then (1) becomes m(2m – 3) = pn, which implies m = pr for some r ≥ 1, and
2pr – 3 = pn–r. (3)
- n – r = 0. By (3) we have r = n = 1 and p = 2; thus, k = 3, pn = 2.
- n – r ≥ 1. Divisibility arguments applied to (3) again imply that p = 3, whence equation (3) becomes 2·3r–1 – 1 = 3n-r–1. Again either 3r–1 or 3n-r–1 must be 1. Here these conditions are equivalent giving us r = 1 and n = 2, and therefore,
k = 5, pn = 9.
|

