|
Solution for January 2009
| The Problem: |
 |
MP83 January 2008
Let a0 = 2009 and 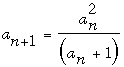 for any non-negative integer n. Prove that 2009 – n is the greatest integer less than or equal to an for 0 ≤ n ≤ 1005. for any non-negative integer n. Prove that 2009 – n is the greatest integer less than or equal to an for 0 ≤ n ≤ 1005.
|
Correct responses: |
 |
This month's problem is a modified version of short-listed problem A1 proposed for the 35th International Mathematical Olympiad (Hong Kong, 1994). Correct solutions were submitted to us by
Bojan Basic (Serbia) |
Seb Lebre (?) |
Luigi Bernardini (Italy) |
Matthew Lim (USA) |
Lou Cairoli (USA) |
Jeff Lindstrom (Ontario) |
Bernard Carpentier (France) |
Catherine Nadault (France) |
Bernard Collignon (France) |
Shpetim Rexhepi (Macedonia) |
Olivier Cyr (France) |
John T. Robinson (USA) |
Philippe Fondanaiche (France) |
Heri Setiyawan (Indonesia) |
Cornel Gruian (Rumania) |
Albert Stadler (Switzerland) |
Omran Kouba (Syria) |
|
|
The solution:
All the solutions had much in common: It follows quickly from the definition that an is positive for all n; also
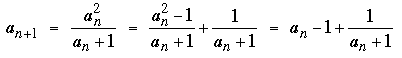 , ,
whence
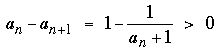
From this we deduce that the sequence is decreasing: a0 > a1 > ... > an > ... . Moreover, we havefor all n > 0,
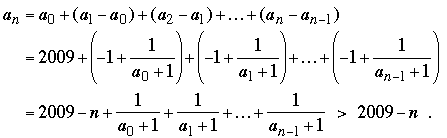 (1) (1)
Let dn = an – (2009 – n). If we can show that the difference dn < 1 for n ≤ 1005, then we can conclude that 2009 – n is the greatest integer less than or equal to an, as claimed. From the third equation in (1),
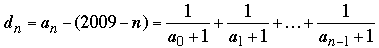 (2) (2)
Again, because the sequence of ak's is decreasing we have 1/(ak + 1) < 1/(an–1 + 1) for k < n – 1. From (1), which says that a1004 > 2009 – 1004 = 1005, we see that for 0 ≤ n ≤ 1005,
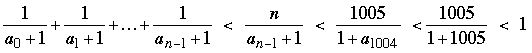 , ,
which completes the argument.
Comments. Even for values of n well beyond 1005 it is clear that 2009 – n is the greatest integer less than or equal to an (in symbols, 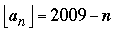 ). Several correspondents investigated how far this equality continues to hold. For the answer one must look more closely at the precise value of the difference dn = an - (2009 - n),
which by (2) is ). Several correspondents investigated how far this equality continues to hold. For the answer one must look more closely at the precise value of the difference dn = an - (2009 - n),
which by (2) is
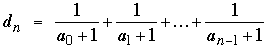
Because an is positive and decreasing to zero, the series on the right grows without bound; thus, there must exist an integer, call it N, for which dN < 1 while dN+1 > 1. Indeed, a computer tells us that N = 1271; that is,
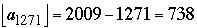 , while , while 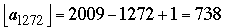
Lim, Kouba, Nadault, Stadler, Fondanaiche and Robinson all showed that if one knows some calculus, it is easy to determine without a computer that N must be either 1270 or 1271. Here is Lim's argument (with contributions from each of the others).
An upper bound on N. (We use the definition of N: for k ≤ N, ak – (2009 – k) < 1; that is, ak < 2010 – k).)
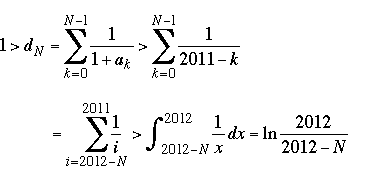
whence 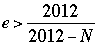 , and therefore , and therefore
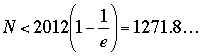
A lower bound on N. (Here we use that for k ≤ N, 1 + (ak – (2009 – k)) > 1; that is, 1 + ak > 2010 – k.)
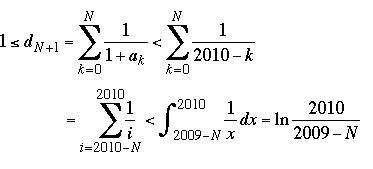
whence 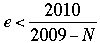 , and therefore , and therefore
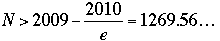
To eliminate 1270 as a possible value for N we need a better estimate for the lower bound. The work is not so much harder, but only Nadault persevered. We have posted her lovely argument on our French web page for those who would like to see the details.
|

