|
Solution for October 2008
| The Problem: |
 |
MP80 October 2008
Find the longest sequence of real numbers such that the sum of every 7 consecutive terms is positive while the sum of every 11 consecutive terms is negative.
|
Correct responses: |
 |
Correct solutions were submitted by
Bojan Basic (Serbia) |
Matthew Lim (USA) |
Gérad Billion (France) |
John T. Robinson (USA) |
Lou Cairoli (USA) |
K. Sengupta (India) |
Sébastien Dumortier (France) |
Javier Rodríguez Soler (Spain) |
Philippe Fondanaiche (France) |
Albert Stadler (Switzerland) |
Farid Alberto Lian Martínez (Colombia) |
|
Our October problem is a slightly modified version of problem 2 from the 1977 International Mathematical Olympiad (see International Mathematical Olympiads 1959-1977, edited by Samuel L. Greitzer; Mathematical Association of America, New Mathematical Library No. 27, 1978).
|
The solution:
Solution. Any sequence that satisfies both
the sum of every 7 consecutive terms is positive, (1)
and
the sum of every 11 consecutive terms is negative (2)
can have at most 16 terms. To prove this, we must first show that any sequence of 17 or more terms cannot satisfy both conditions, and then we must provide an example of a sequence of 16 terms that does satisfy both conditions. (Any such example will automatically furnish examples of suitable sequences of length n with n < 16.) Our correspondents devised three nice approaches to the problem.
Method 1.
If, to the contrary, the two conditions were satisfied by a sequence of 17 terms a1, a2, ..., a17, then we could arrange the subsequences of length 7 in the rows of an 11 by 7 array,
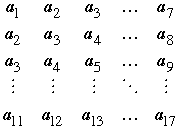
By condition (1), the sum of all the entries taken a row at a time must be positive; that same sum taken a column at a time must be negative by (2). This tells us that no sequence having the desired properties can have length 17 or more.
For an example of a suitable sequence having 16 terms, we can let the 10 row sums aj+1 + aj+2 +...+
aj+7 be any positive numbers (for j running from 0 to 9); for simplicity, let all ten sums be 1. By subtracting successive pairs of these sums, for example,
(a2 + a3 +
a4 + a5 +
a6 + a7 +
a8) -
(a1 + a2 +
a3 + a4 +
a5 + a6 +
a7)
= a8 - a1 = 1 - 1 = 0,
we deduce that aj = aj+7 for 1 ≤ j ≤ 9. Similarly, we can let the sums
aj+1 + aj+2 + ... + aj+11 be any negative numbers (for j running from 0 to 5); let these sums be –1, say. From these six equations we deduce that aj = aj+11. These equalities imply that every subsequence of seven consecutive terms will contain five a1's and two a3's, while subsequences of eleven consecutive terms will contain eight a1's and three a3's; therefore,
5a1 + 2a3 = 1 and 8a1 + 3a3 = -1,
whence, a1 = –5 and a3 = 13. The resulting sequence of 16 terms is then
–5, –5, 13, –5, –5, –5, 13, –5, –5, 13, –5, –5, –5, 13, –5, –5.
Method 2. Bojan Basic's approach.
Basic, Fondanaiche, Lim, and Sengupta all generalized our problem. They found that for any two positive integers m and n, the longest possible sequence of real numbers for which the sum of every m consecutive terms is positive while the sum of every n consecutive terms is negative has, in terms of the greatest common divisor (gcd(m, n)),
m + n – gcd(m, n) – 1 terms. (3)
We shall use Bojan Basic's idea of defining a sequence of partial sums Sj by
S0 = 0, S1 = a1, S2 = a1 + a2, …, Sj = a1 + a2, …,+ aj .
Instead of presenting a general argument, we will illustrate the method by way of three examples.
Example 1. Take m = 3 and n = 5. We show that the longest sequence has 3+5–1–1 = 6 terms in agreement with (3).
"The sum of every 3 consecutive terms is positive" is equivalent to Sj < Sj+3 ,
while
"The sum of every 5 consecutive terms is negative" is equivalent to Sj+5 < Sj.
To show that no sequence satisfying these conditions can have 7 or more terms, we assume to the contrary that a1, a2, …, a7 is such a sequence. Consider the following chain of inequalities:
0 < S3 < S6 < S1 < S4 < S7 < S2 < S5 < 0 (4)
This contradiction 0 < 0 proves that any sequence satisfying the two conditions of this example must have fewer than 7 terms. Note that in (4) we took the chain of inequalities as far as possible using the condition Sj < Sj+3 (S6 < S9 is not valid since S7 is the longest partial sum), and then we brought the indices back with as many applications of the second condition Sj+5 <Sj as possible. The fastest way to bring the indices back to 0 is to use the positive partial sums n = 5 times and the negative partial sums m = 3 times.
How to get an example with six terms? Start the chain to the right of S7 in (4):
S2 < S5 < 0 < S3 <S6 <S1 <S4 (5)
Any assignment of real values to the Si that satisfies (5) will produce a sequence of six terms that satisfies the initial conditions; for example, S2 can be any negative real number, and S5 any number between that and 0. If we set S2 = –2, S5 = –1, S3 = 1, S6 = 2, S1 = 3, and S4 = 4, then use the definitions S1 = a1 and aj+1 = Sj+1 – Sj, our sequence will be 3, –5, 3, 3, –5, 3. Because this sequence was chosen to satisfy (5), we know that the sum of any three consecutive terms is positive (here that sum is always 1), while any five consecutive terms have a negative sum (here –1).
Example 2. Take m = 4 and n = 6. Since gcd(4, 6) = 2, we expect the longest sequence to have 4+6–2–1 = 7 terms in agreement with (3). We now have
0 < S4 < S8 < S2 < S6 < 0
which shows that our sequence cannot have 8 or more terms. (Here we brought the indices back to 0 by using Sj < Sj+4 only 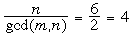 times, while Sj+6 < Sj we used times, while Sj+6 < Sj we used 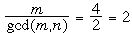 times.) To produce a valid sequence of seven terms we use the above chain without S8, namely S2 < S6 < 0 < S4 , together with the remaining conditions S3 < S7 < S1 < S5. Because these conditions are necessary and sufficient, S2 can be assigned any negative value while S3 is completely arbitrary. Taking S2 = – 2, S6 = –1, S4 = 1, S3 = 0, S7 = 1, S1 = 2, and S5 = 3, our sequence starts with S1 = a1 = 2, and is thus 2, –4, 2, 1, 2, –4, 2. times.) To produce a valid sequence of seven terms we use the above chain without S8, namely S2 < S6 < 0 < S4 , together with the remaining conditions S3 < S7 < S1 < S5. Because these conditions are necessary and sufficient, S2 can be assigned any negative value while S3 is completely arbitrary. Taking S2 = – 2, S6 = –1, S4 = 1, S3 = 0, S7 = 1, S1 = 2, and S5 = 3, our sequence starts with S1 = a1 = 2, and is thus 2, –4, 2, 1, 2, –4, 2.
Example 3. The original problem: Take m = 7 and n = 11. Since gcd(7, 11) = 1, we expect the longest sequence to have 7+11–1–1 = 16 terms in agreement with (3). Because 7 and 11 are relatively prime, any sequence of 17 consecutive terms produces a single chain of inequalities,
0 < S7 < S14 < S3 < S10 < S17 < S6 < S13 < S2 < S9 < S16 < S5
< S12 < S1 < S8 < S15 < S4 < S11 < 0.
For an example with 16 terms we drop S17 from the above chain (start with S6 and end with S10). So to recover the sequence –5, –5, 13, –5, … we had earlier, we set S6 = –12 and let each Sj in the chain be 1 greater than the previous partial sum in the chain.
Method 3. Use Matrices.
Several correspondents implicitly used matrices; Billion supplied the explicit matrices. To illustrate the idea we will first work a small example with m = 2 and n = 3; that is, we want aj + aj+1 to be positive for all j and aj + aj+1 + aj+2 to be negative. We expect the longest sequence to have 2+3–2 = 3 terms. We summarize this information with the matrix equation
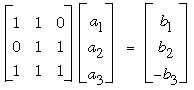
where the bj's can be assigned any positive values. Let us take bj = 1 for all j, and solve the equation by computing the inverse matrix, which exists because the above matrix is clearly nonsingular:
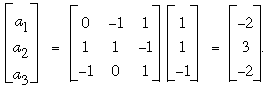
We read off the desired sequence in the last column: –2, 3, –2. By observing that the matrix in the preceding equation will take 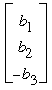 to to 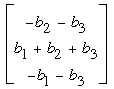 , we see that any assignment of positive values to the bj's will produce a sequence aj, aj+1, aj+2 in the order negative, positive, negative. Were there to exist a sequence longer than three terms that satisfied the given conditions, say a1, a2, a3, a4, …, then we know that a2 would necessarily be positive as part of the triple a1, a2, a3, but it would necessarily be negative as part of the triple a2, a3, a4. Since the pattern – + – cannot be preserved for all j in a sequence of more than three terms, we see that, indeed, the longest sequence satisfying the given conditions has three terms. , we see that any assignment of positive values to the bj's will produce a sequence aj, aj+1, aj+2 in the order negative, positive, negative. Were there to exist a sequence longer than three terms that satisfied the given conditions, say a1, a2, a3, a4, …, then we know that a2 would necessarily be positive as part of the triple a1, a2, a3, but it would necessarily be negative as part of the triple a2, a3, a4. Since the pattern – + – cannot be preserved for all j in a sequence of more than three terms, we see that, indeed, the longest sequence satisfying the given conditions has three terms.
For his solution to the original problem (with m = 7 and n = 11) Billion used the matrix equations MA = B, and A = M–1B, with
M =  , ,
M-1 =  , ,
A = [a1, a2, …, a16]t, and B = [b1, b2, …, b10, –b11, …, –b16]t. With bj = 1 for all j, he recovered our sequence
A = [–5, –5, 13, –5, –5, –5, 13, –5, –5, 13, –5, –5, –5, 13, –5, –5]t.
With bj = 2 for j ≤ 10 and bj = 3 for j > 10, he found that
A = [–12, –12, 31, –12, –12, –12, 31, –12, –12, 31, –12, –12, –12, 31, –12, –12]t
is likewise a suitable sequence. Once again we see that any sequence of more than 16 terms could not satisfy the given conditions: a3 would necessarily be positive in the subsequence a1, a2, a3, …, a16, but negative in the subsequence a2, a3, a4, …, a17.
|

