|
Solution for April 2010
| The Problem: |
 |
What can you say about the angles of a triangle having the property that when you divide the sum of the cubes of the sides by its perimeter, you get the area of the square on one of its sides?
|
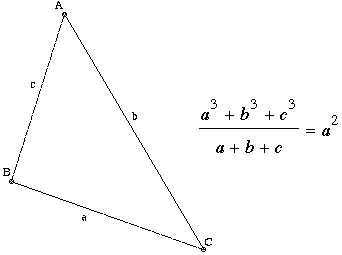
Correct responses: |
|
Our April problem came from a list of problems that Murray Klamkin proposed for the 1983 Canadian Math Olympiad. Correct solutions were submitted to us by
Bahman Ahmadi
(Regina) |
Sébastien Dumortier
(France) |
Farid Alberto Lian Martínez
(Colombia) |
Halima Bashier
(Regina) |
Amit Elazari |
Remo Mantovanelli
(Italy) |
Bojan Basic
(Serbia) |
Mei-Hui Fang
(Austria) |
Milan Pavic
(Serbia) |
Luigi Bernardini
(Italy) |
Constantin Fishkin
(Ontario) |
Arnaud Piquerez
(France) |
José Borges
(Portugal) |
Philippe Fondanaiche
(France) |
John T. Robinson
(USA) |
Bernard Carpentier
(France) |
Bruce Golfman
(Austria) |
Albert Stadler
(Switzerland) |
Bernard Collignon
(France) |
Cornel Gruian
(Romania) |
A. Teitelman
(Israel) |
Andrew Cooke
(China) |
Benoît Humbert
(France) |
Jan van Delden
(The Netherlands) |
Shai Covo
(Israel) |
Magnus Jakobsson
(Sweden) |
Ray Van Raamsdonk
(British Columbia) |
Dan Dima
(Romania) |
Wolfgang Kais
(Germany) |
Benjamin Louradour
(France) |
Allen Druze
(USA) |
Normand LaLiberté
(Ontario) |
 KURIHARA Tomohiro
(Japan)
|
We also received five incorrect submissions this month.
|
The solution:
We will see that when ΔABC is labeled so that the angle at A is opposite the side on which you get the area of the square, then ∠A = 60°. The measures of other two angles can be any pair of positive numbers whose sum is 120°.
Starting with the given quotient, we get, in turn,
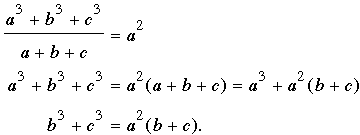
Since b3 + c3 = (b2 - bc + c2)(b + c) and b + c > 0 (because the lengths of the sides of a triangle are positive by definition), the last equation becomes
b2 - bc + c2 = a2.
The Cosine Law says that a2 = b2 + c2 - 2bc cos A, so equating our two expressions for a2 gives us – bc = –2bc cos A, or
cos A = 1/2.
Because the angles of a triangle measure between 0° and 180°, ∠A = 60°, as claimed. Conversely, because all the steps are reversible, if ∠A = 60°, then  .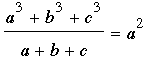
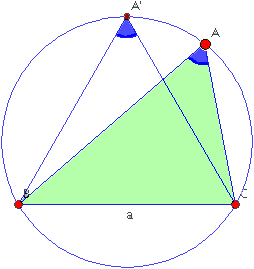
Triangle A'BC in the accompanying figure is equilateral. By clicking on the figure you will get an applet in which the vertex A can be moved about the upper arc BC of the circle; as it moves, you get to see all triangles with the desired property that have a = BC as one of its sides. Note that as A moves its measure remains fixed at 60°; although B and C vary in size, they always sum to120°. Similarly, the side lengths b and c vary as A moves, but the Cosine Law implies that b2 + c2 - 2bc cos A and, therefore 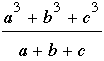 are both constant and equal to a2.
|
