Solution for February 2010

The Problem:

The eleven members of the local football team gather at the pub after each game. Afterwards, they roll a pair of dice to determine who picks up the tab. Happily, the numbers on their jerseys run from 2 to 12, so the player whose jersey number matches the sum that shows on the dice pays the bill. But even a football player realizes that the eleven sums are not equally likely. Your task this month is to help make the process fair: Describe how to load a pair of dice, one red, one green, so that every sum from 2 to 12 is equally likely, or prove that it is impossible.

Correct responses:

Correct solutions were submitted this month by Claudio Baiocchi (Italy) Bruce Golfman (Austria) Bojan Basic (Serbia) Cornel Gruian (Romania) Luigi Bernardini (Italy) Benoît Humbert Lou Cairoli (USA) David Jackrel (USA) Bernard Collignon (France) Magnus Jakobsson (Sweden) Shai Covo (Israel) Normand LaLiberté (Ontario) Jan van Delden (The Netherlands) Matthew Lim (USA) Allen Druze (USA) Claude Morin (France) Mei-Hui Fang (Austria) Vincent Pantaloni (France) Philippe Fondanaiche (France) John T. Robinson (USA) Tom Fuzesy (Regina) Ray Van Raamsdonk

The solution:

            We first must agree upon what it means to "load a pair of dice."  A traditional die is a small cube with each face having a different number of spots on it, from 1 to 6.  The die is said to be fair if, when it comes to a rest after having been properly rolled, each side has a probability of 1/6 of facing upwards.  The die is loaded if it has been tampered with so that some of the probabilities for the up-faces are different from 1/6, perhaps from its edges having been shaved or from weights having been inserted.  Some of our correspondents, however, interpreted loaded dice to refer to dice that have been modified in any way.  This more general interpretation leads to a different, but interesting problem, which we discuss later.
            We assume that the dice have been loaded so that the probability that for 1 ≤ i, j ≤ 6, the red face numbered i appears with probability r_i, while the green face numbered j appears with probability g_j.  When the dice are rolled (which implies that the outcomes for the two dice are independent), r_ig_j is the probability that the red die comes up i and the green die comes up j.  For each n from 2 to 12 we denote by S_n the probability of rolling a total of n, and we obtain that probability by summing the product r_ig_j over all i and j for which i + j = n.  So, for example,

S₂ = r₁g₁;   S₇ = r₁g₆ + r₂g₅ + r₃g₄ + r₄g₃ + r₅g₂ + r6g₁;   and S₁₂ = r₆g₆.

            We need one more preliminary fact.  For any number x greater than zero,

.

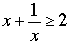It is a simple calculus exercise to establish this inequality but, of course, calculus is not needed:  simply note that

,

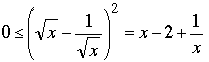then take the –2 to the other side.  Equality holds if and only if x = 1.
            We now show by two methods that it is not possible to load the dice so that all eleven possible values of n are equally likely. 

Method 1.  It is not even possible to arrange values of r_i  and g_j so that S₂ = S₇ = S₁₂ = 1/11.  Assume that r₁g₁ = r₆g₆ = 1/11.  Then

,

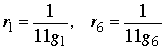and, consequently,

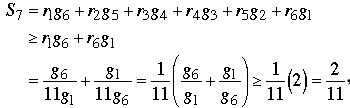
where for the first inequality we used the fact that probabilities cannot be negative, and for the last inequality we used the preliminary fact with x = g₆/g₁.  In words, if S₂ and S₁₂ both equal 1/11, then S₇ must equal 2/11 or more — there is no way for S₇ to equal 1/11. 

Comments.
            Cairoli and Covo both avoided appealing to the preliminary fact as follows: Were we, to the contrary, to have S₇ = 1/11 = r₁g₁, the first inequality above would say that

r₁g₁ ≥  r₁g₆ + r₆g₁;

since none of the terms in this inequality can be zero, r₁g₁ >  r₁g₆ implies that g₁ > g₆, while r₁g₁ > r₆g₁ implies r₁ > r₆, which together imply that r₁g₁ > r₆g₆, and that contradicts the assumption that both these products are equal to 1/11.
            Several correspondents commented that Method 1 can be applied to dice with any number of sides: s-sided dice (whose faces are numbered from 1 to s) cannot be loaded so that the outcomes 2, 3, ..., 2s are equally likely.  In particular, a pair of coins whose sides are labeled 1 and 2 cannot be weighted so that the outcomes 2, 3, and 4 become equally likely.

Method 2.  This is an easy approach for those who are familiar with generating functions.  The argument works for dice with any even number of sides, but we shall stay with our 6-sided loaded dice and their probabilities r_i and g_j.  Set

R(x) = r₁x + r₂x² + r₃x³ + r₄x⁴ + r₅x⁵ + r₆x⁶

and

G(x) = g₁x + g₂x² + g₃x³ + g₄x⁴ + g₅x⁵ + g₆x⁶.

The coefficient of x_n in the product R(x)·G(x) is the probability S_n of rolling a total of n with the pair of loaded dice; that is,

R(x)·G(x) = S₂x² + S₃x³ + S₄x⁴ + ... + S₁₂x¹².

The question is whether it is possible that all the coefficients can equal 1/11; that is, can

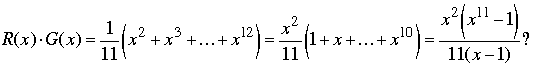
But, this equality is impossible because R(x)/x and G(x)/x are 5^th degree polynomials, which implies that they each have at least one real root; on the other hand, 1 + x + ... + x¹⁰ has no real roots (because its roots are the eleventh roots of unity different from 1).  Thus the product of the polynomials on the left cannot equal the polynomial on the right, as claimed.

Modifications that lead to equal values of S_n for n from 2 to 12.
Change the numbers on the faces of the red die.  For example you can arrange for the odd faces each to have a single spot (by removing all but the centre spot), and for the even faces each to have seven spots (by adding the appropriate number of spots).  Then there is an equal chance of rolling a red 1 (in which case the totals from 2 to 7 would be equally likely) or a red 7 (in which case the totals from 8 to 13 would be equally likely).  If a thirteen results, then the dice must be rolled again or, as our more practical-minded correspondents suggest, the team could invite the bar tender or the coach to participate as number 13.

Remove the independence condition. Baiocchi proposes that the dice be rolled separately.  First roll the green die which has been loaded so that r₁ = 6/11 while the other five faces appear with probability 1/11.  If a 1 has been rolled, then roll an ordinary red die (in which case the totals 2 through 7 each have a probability of 1/11); but if any other number appears on the green die, then exchange the fair red die with one for which the number 6 is rolled with probability 1.

Modify the procedure. Finally, Covo suggests that a pair of fair dice be rolled repeatedly until a 1 appears on the red die or a 6 appears on the green.  Since there are 11 ways this can happen (out of the 36 equally likely outcomes from rolling a pair of fair dice), and each way has a different sum, the probability of rolling a particular total from 2 to 12 equals 1/11, as desired.