|
Solution for January 2010
| The Problem: |
 |
Show that the product
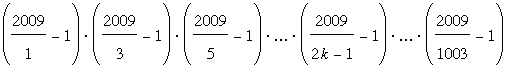
is a power of 2.
|
Correct responses: |
 |
Correct solutions were submitted this month by
Berkay Anahtarci
(Turkey) |
Mei-Hui Fang
(Austria) |
Remo Mantovanelli
(Italy) |
Claudio Baiocchi
(Italy) |
Philippe Fondanaiche
(France) |
Claude Morin
(France) |
Halima Bashier
(Regina) |
Tom Fuzesy
(Regina) |
Milan Pavic
(Serbia) |
Bojan Basic
(Serbia) |
Bruce Golfman
(Austria) |
Shpetim Rexhepi
(Macedonia) |
Luigi Bernardini
(Italy) |
Patrick Gordon
(France) |
Eric Reynaud
(France) |
José Borges
(Portugal) |
Cornel Gruian
(Romania) |
John T. Robinson
(USA) |
Lou Cairoli
(USA) |
David Jackrel
(USA) |
Heri Setiyawan
(Indonesia) |
John Campbell
(Alberta) |
Magnus Jakobsson
(Sweden) |
Nutheti Shivdeep
(India) |
Bernard Carpentier
(France) |
Wolfgang Kais
(Germany) |
A. Teitelman
(Israel) |
Bernard Collignon
(France) |
Stephen La Rocque
(Ontario) |
Jan van Delden
(The Netherlands) |
Olivier Cyr
(France) |
Normand LaLiberté
(Ontario) |
Ray Van Raamsdonk
(British Columbia) |
Allen Druze
(USA) |
Daniel Lu
(USA) |
Leonardo Vicchi
|
| |
Karim Laaouini
(Marocco) |
|
We will start with a proof that was common to many of the solutions sent to us this month. We follow that by two approaches to a generalization that is no harder than the original problem, and we end with two further generalizations.
|
The solution:
The original problem.
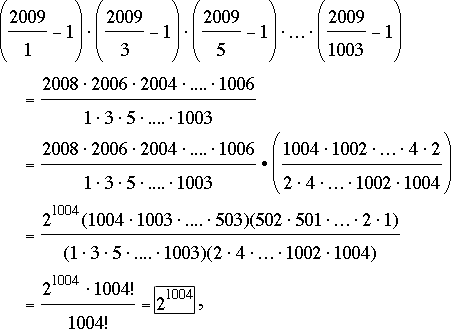
which is a power of 2, as desired.
A generalization. Ten of our correspondents observed that the number 2009 could be replaced by 4n + 1 in the statement of our problem; specifically, for all integers n ≥ 1,
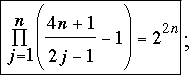 (1) (1)
in the original problem we have n = 502. Bernardini, Colignon, Golfman, Gruian, Morin, and van Delden applied a version of the argument we presented above; namely,
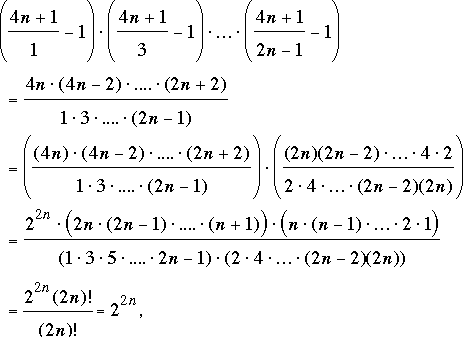
as claimed.
Mathematical induction. Basic, Fondanaiche, La Liberté, and Vicchi let P(n) stand for the product on the left side of equation (1), and they used induction to prove that P(n) = 22n. P(1) is simply 5 – 1 = 22, so assume that P(k) =
22k; we are to prove that P(k + 1) =
22(k+1).
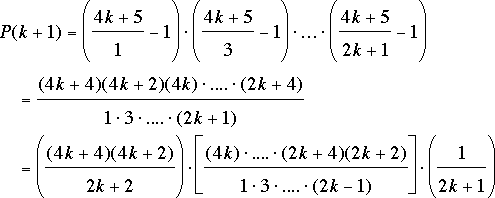
where we inserted the term 2k + 2 in both the numerator and the denominator. Note that the expression in the square brackets is P(k), which we have assumed to equal 2k. Thus,
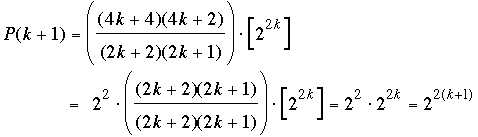
as was to be proved.
Comments. We thank our colleague Richard McIntosh for suggesting this month's problem. He recently discovered equation (1) and several related identities in his investigation of Bernoulli and Euler numbers that will be incorporated into a forthcoming article. In fact, a version of equation (1) holds also for 4n – 1, namely
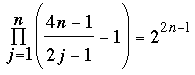 , n ≥ 1. (2) , n ≥ 1. (2)
Furthermore, there is a similar identity with a plus sign in the product, namely
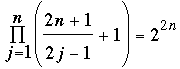 , n ≥ 1. (3) , n ≥ 1. (3)
Identities (2) and (3) can both be proved using the same methods that worked for (1).
|

