Solution for March 2010

Math Central - mathcentral.uregina.ca

Problem of the Month

Current
problem

Recent problems
with solutions

Older problems from
2005/2006	06/07	07/08	08/09	09/10	10/11	11/12

Solution for March 2010

The Problem:

Here is a 3-part problem for month number 3:

Can you find integers s and t, both greater than 1, for which (s^s)² = t^t?
Can you find integers s and t, both greater than 1, for which ( s^s)²⁰¹⁰ = t^t?
Can you find integers s and t, both greater than 1, for which s^{(s²⁰¹⁰)} = t^t?

Correct responses:

The source for our March problem was Stan Wagon's "Problem of the Week" number 1038 (from September 26, 2005). Solutions were submitted to us by

Bojan Basic (Serbia)	Magnus Jakobsson (Sweden)
Shai Covo (Israel)	Wolfgang Kais (Germany)
Mei-Hui Fang (Austria)	Matthew Lim (USA)
Philippe Fondanaiche (France)	John T. Robinson (USA)
Cornel Gruian (Romania)	Jan van Delden (The Netherlands)
Benoît Humbert	Ray Van Raamsdonk

A few of these solutions contained unsubstantiated claims that led to faulty conclusions. Because their arguments were essentially correct, we have included the authors' names in the above solver list, but we remind everybody that in mathematics one must make certain that every claim is correct and backed by a valid argument.

The solution:

Part a. No, there are no integers s and t greater than 1 for which (s^s)² = t^t.

Note first that (s^s)² = s^2s. Should there exist such a pair s and t, then on the one hand because s,t >1 we get s^s < s^2s = t^t, whence s < t; on the other hand, t^t = s^2s < (2s)^(2s), so that t < 2s. But t < 2s implies that s^t divides evenly into s^2s = t^t, whence s would necessarily divide evenly into t; however s < t < 2s tells us that to the contrary, the smallest multiple of s is greater than t, so that s cannot divide evenly into t. This contradiction implies the nonexistence of our desired pair of integers.

Part b. Yes, there are many possible pairs; for example,

s = 1005 and t = 10052

and

s = 2009²⁰⁰⁹ and t = 2009²⁰¹⁰.

To discover the first pair we have

(s^s)²⁰¹⁰ = s^2010s = s^2·1005s = (s²)^1005s,

which is in the form t^t if we set s² = 1005s; that is, s = 1005.

Comment. Note that this trick works for all even exponents except 2:

for all integers k > 1, (s^s)^2k = t^t when s = k and t = k².

Try it with k = s = 2 and t = 4: (2²)⁴ = 2⁸ = 4⁴.

Later we will see where the second pair comes from. For now let us be satisfied in observing that

for all integers n > 2, (s^s)ⁿ = t^t when s = (n – 1)^n–1 and t = (n – 1)ⁿ.

Thus, in the smallest case n = 3 we have s = 2² = 4, t = 2³ = 8, and

(s^s)³ = (2²)^3·2² = (2³)^2·2² = (2³)^(2³); that is, 4¹² = 8⁸.

For our problem n = 2010, s = 2009²⁰⁰⁹, and t = 2009²⁰¹⁰:

(s^s)²⁰¹⁰ = (2009²⁰⁰⁹)^{2010·2009²⁰⁰⁹} = (2009²⁰¹⁰)^{2009·2009²⁰⁰⁹}
= (2009²⁰¹⁰)^{(2009²⁰¹⁰)} = t^t.

In general,

(s^s)ⁿ = ((n-1)^n-1)^{n·(n-1)^n-1} = ((n-1)ⁿ)^{(n-1)·(n-1)^n-1} = ((n-1)ⁿ)^((n-1)ⁿ) = t^t.

Comment. We have here what might be called an anti-Fermat theorem: It has no solution in integers when the exponent is 2, yet many solutions when the exponent is an integer greater than 2; moreover, the proof would fit in the margin of Fermat's book.

Part c. Yes, there is a satisfactory pair:

s = 2009, t = 2009²⁰⁰⁹.

We have

s(^s²⁰¹⁰) = s^{s·(s²⁰⁰⁹)} = (s^s)^{(s²⁰⁰⁹)}.

To get this in the form t^t we can let s = 2009. Similarly,

for any n>2, (s^s)ⁿ = t^t when s = n-1 and t = (n-1)^(n-1).

So, for example, when n = 3, s = 2, and t = 2² = 4 we again have 2^(2³) = 4⁴.

Further observations.

Kais and Lim investigated whether it might be possible to determine all solutions in the general settings of parts (b) and (c). For part (b) we fix a positive integer n, and ask which pairs of integers s, t ≥ 2 satisfy (s^s)ⁿ = t^t. We shall obtain a partial solution to the question by adopting the very simple argument of Jakobsson, who was concerned only about finding a suitable approach to the problem as we stated it. It is clear that s and t must both have the same prime divisors; we will find all those solutions where there exists a common divisor a such that s = a^k and t = a^m for integers k and m. Because (s^s)ⁿ = t^t holds if and only if a^{kna^k} = a^{ma^m}, it holds if and only if kna^k = ma^m. We deduce that there exists a solution pair s and t that are powers of the same integer a if and only if there exist integers k and m with m > k and

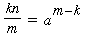It is clear that if we take m to be any divisor greater than 1 of our given exponent n, there will be a solution with k = m – 1, namely

eqn 2

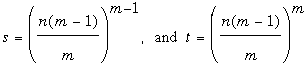
In particular, when we take m = n we get the solution s = (n – 1)^n–1, t = (n – 1)ⁿ that we verified above. When n has proper divisors, there are further choices for m. Using n = 2010 as an example, we see that 2010 = 2·3·5·67, so n has 15 divisors m greater than 1, all of which lead to a solution:

m	2010	1005	670	402	335	201	134	67
n/m	1	2	3	5	6	10	15	30
s	2009²⁰⁰⁹	2008¹⁰⁰⁴	2007⁶⁶⁹	2005⁴⁰¹	2004³³⁴	2000²⁰⁰	1995¹³³	1980⁶⁶
t	2009²⁰¹⁰	2008¹⁰⁰⁵	2007⁶⁷⁰	2005⁴⁰²	2004³³⁵	2000²⁰¹	1995¹³⁴	1980⁶⁷

m	30	15	10	6	5	3	2
n/m	67	134	201	335	402	670	1005
s	1943²⁹	1876¹⁴	1809⁹	1675⁵	1608⁴	1340²	1005
t	1943³⁰	1876¹⁵	1809¹⁰	1675⁶	1608⁵	1340³	1005²

So, for example,

(1943²⁹)^(1943²⁹)²⁰¹⁰ = (1943²⁹)^{30·67·(1943²⁹)} = (1943³⁰)^{29·67·(1943²⁹)}
= (1943³⁰)^{1943·(1943²⁹)} = (1943³⁰)^(1943³⁰)

Kais used his computer to show that when n = 2010 there are just these 15 solutions, and no others. Both he and Lim showed that, on the other hand, there can be other possibilities for appropriate values of n. For example, when n = 11 we can take m = 11 and let k be 8 or 9 (as well as our canonical k = m – 1 = 10) :

Given n = 11, take m = 11 and k = 8; then kn/m = 8 = a^11–8 = a³; thus a = 2, s = 2⁸, t = 2¹¹.
Given n = 11, take m = 11 and k = 9; then kn/m = 9 = a^11–9 = a²; thus a = 3, s = 3⁹, t = 3¹¹.
Given n = 11, take m = 11 and k = 10; then kn/m = 10 = a; thus s = 10¹⁰, t = 10¹¹.

Kais's computer showed that there were no further solutions when n = 11.

For further solutions to (s^s)ⁿ = t^t, we again set s = a^k and t = a^m. This now leads to

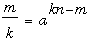
For n > 2 the choice of k = 1, m = n – 1, leads to the solution a = n – 1; whence, s = n – 1 and t = (n – 1)^n–1. Kais proved that there can be no solution when n = 2, and he showed (by computer) that the choice k = 1 produces the unique solution when n = 2010 that we have given above. Also here, for the exponent n = 11 there are three solutions with k = 1, and none for other values of k: for m = 8 we have s = 2, t = 2⁸; for m = 9 we have s = 2, t = 2⁹; and for m = 10 we have s = 2, t = 2¹⁰.

Finally, we note that for fixed n, any solution to (s)^sⁿ= t^t leads to a solution to (S^S)ⁿ = T^T by setting S = t and T = sⁿ: (S^S)ⁿ = ( t^t)ⁿ = (s^(sⁿ))ⁿ = s^n(sⁿ) = (sⁿ)^(sⁿ) = T^T. You cannot go in the other direction however: we have seen that there are generally more solutions in part (b) than there are in part (c), so it is clear that solutions to (S^S)ⁿ = T^T do not lead in an obvious way to solutions of (s)^sⁿ= t^t.

Math Central is supported by the University of Regina and the Pacific Institute for the Mathematical Sciences.