Note that we now allow r to be p – 1, but not 0, so that by definition (p – 1)K < n. The case p = 2 reduces to the observation that for p = 2 and any positive integer n, r = 2–1 = 1, K = n – 1, and
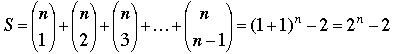 ,
,
which is divisible by 2 as desired. The argument for p ≥ 3 that follows is a composite of similar submissions from Fishkin, Gruian, Haider, Morin, LoPresti, and Stadler. Morin proved our revised statement (as did Fang using a different argument); Gruian proved a result, discussed later, that is yet more general. Our proof is an immediate consequence of two results that are "well known" to those who know them well. If you know them, then you should skip the details and go directly to the argument that follows the proof of the second result.
Result 1. For the prime number p let us denote the power sum 1k + 2k + 3k + … + (p-1)k by Pk. Then
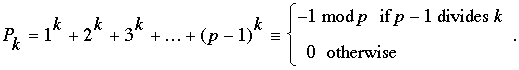 |
Proof. By Fermat's little theorem, for all positive integers a, if p – 1 divides evenly into k, then ak ≡ 1 (mod p), and the sum of p – 1 ones is congruent to –1 (mod p), as claimed. For the other values of k, namely those whose modulus lies strictly between 0 and p – 1, we introduce a primitive root modulo p. This is an integer between 1 and p – 1 whose powers, taken mod p, produce a rearrangement of the integers from 1 to p – 1. So, for example, 3 is a primitive root modulo 7 because the successive powers of 3 taken modulo 7 are 3, 2, 6, 4, 5, 1 (That is, 31 ≡ 3, 32 ≡ 2, 33 ≡ 6, etc.); on the other hand, 2 is not a primitive root modulo 7 because its powers are congruent to 2, 4, 1, 2, 4, 1, and no power of 2 is congruent to 3, 6, or 5 (mod 7). An early theorem of Gauss (whose nontrivial proof is taken up in classes that deal with finite fields or number theory) says that every prime number p has at least one primitive root modulo p. We will denote such a primitive root by g and rewrite Pk as
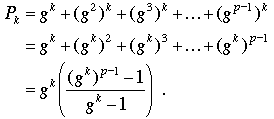
Because we assume here that k is not a multiple of p – 1, the denominator is nonzero while Fermat's little theorem implies that the numerator is zero. That is, Pk = 0 whenever k is not a multiple of p – 1, which completes the proof of the first result.
Result 2.
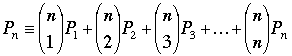 (mod p). (mod p). |
Proof. Working modulo p and using the binomial theorem we have
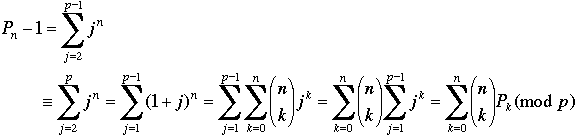
By Result 1, P0 ≡ 1 (mod p), whence the term with k = 0 on the right is 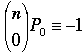 (mod p), and
(mod p), and 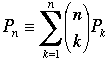 (mod p), as claimed.
(mod p), as claimed.
Readers who are uncomfortable with the summation notation used in the preceding proof might try applying the argument to simple examples such as n = 6 and p = 5:
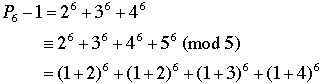
= 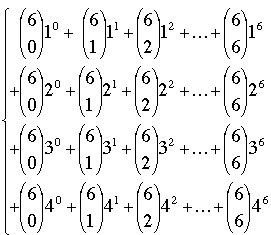
= 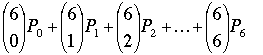
≡ 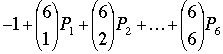 (mod 5).
(mod 5).
Proof of the main result.
We are now ready to prove that S is divisible by p. By Result 1 we can replace P0 on the left side of the congruence in Result 2 by 0 when n is not divisible by p – 1, and by –1 when it is; similarly we replace each Pk on the right, for k from 1 to n, by 0 when k is not divisible by p – 1 and by –1 when it is. When n is not divisible by p – 1 (as in the original statement of the problem), the congruence in Result 2 reads,
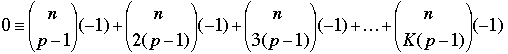 (mod p),
(mod p),
which says that –S ≡ 0 (mod p) or, equivalently, that S is divisible by p. Finally, when n is divisible by p – 1, we set n = K(p – 1) + (p – 1), and the congruence in Result 2 becomes,
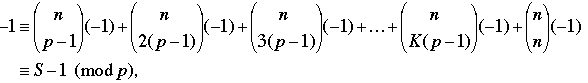
which again says that S is divisible by p.
Further comments.
Our theorem is essentially an 1876 result of Hermite, which itself is a special case of a theorem of J.W.L. Glaisher [A Congruence Theorem Relating to Sums of Binomial-Theorem Coefficients. Quart. J. Math. 30(1899) 150-156, 349-360, 361-383]:
Glaisher's Theorem. For any nonnegative integer K and prime p, if n = (p – 1)K + r, with 1 ≤ r ≤ p – 1, and s is an integer satisfying 1 ≤ s ≤ p – 1, then
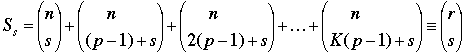 (mod p)
(mod p)
We use the convention that when a > b, 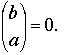 Note that our S is related to Sp–1 by S = Sp–1 – 1. We are grateful to Cornel Gruian (who submitted two proofs) for bringing these references to our attention. Covo, Golfman, and Jakobsson devised results that were special cases of Glaisher's theorem; their proofs were based on induction or on a theorem of Lucas.
Note that our S is related to Sp–1 by S = Sp–1 – 1. We are grateful to Cornel Gruian (who submitted two proofs) for bringing these references to our attention. Covo, Golfman, and Jakobsson devised results that were special cases of Glaisher's theorem; their proofs were based on induction or on a theorem of Lucas.
We will conclude with an argument based on Delay's submission. To follow the argument the reader should be familiar with fields that have p elements, p a prime, denoted by GF(p) or by Z/pZ. (When working over finite fields, the symbol "=" signifies "congruent modulo p", all arithmetic operations are reduced modulo p to an integer from 0 to p – 1, and for all nonzero elements x in the field, xp–1 = 1; consequently, for all x, xa = xb if and only if a ≡ b (mod p – 1). Moreover, every function from GF(p) into itself can be represented in exactly one way by a polynomial of degree at most p – 1.)
Define the polynomial function 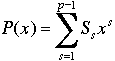 over GF(p). For every x in GF(p),
over GF(p). For every x in GF(p),

We conclude that 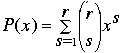 for all x. Since r ≤ p – 1, the coefficient of xs in the definition of P(x), namely Ss, must equal the corresponding coefficient on the right, namely
for all x. Since r ≤ p – 1, the coefficient of xs in the definition of P(x), namely Ss, must equal the corresponding coefficient on the right, namely 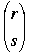 , as claimed.
, as claimed.

