|
Solution for October 2009
| The Problem: |
 |
MP89 October 2009
A knockout tournament is a competition consisting of multiple rounds. In each round the competitors are paired up; the winner of each pairing moves on to the next round while the loser is eliminated. A bye is given to a competitor who has no assigned opponent, which means that he passes directly to the next round. We are interested in the minimum possible number of byes in a tournament having n contestants. For example, when there are 6 contestants, the tournament might have two byes in the first round, or it can have no byes in the first round and just one bye in the second round. The minimum number of byes in a tournament having 6 contestants is therefore one.
- What is the minimum number of byes in a knockout tournament with 2010 contestants?
- Because of a doping scandal only 1025 contestants were able to compete in the tournament. How many byes did there have to be in the new draw?
|
Correct responses: |
 |
Correct solutions were submitted this month by
| Claudio Baiocchi (Italy) |
Omran Kouba (Syria) |
Halima Abdalla Bashier (Regina) |
Tannie Lau |
Bojan Basic (Serbia) |
Matthew Lim (USA) |
José Borges (Portugal) |
Jeff Lindstrom (Ontario) |
Lou Cairoli (USA) |
John T. Robinson (USA) |
Dan Dima (Romania) |
Uwe Schaefer (Germany) |
Sébastien Dumortier (France) |
Nutheti Shivdeep (India) |
Magnus Jakobsson (Sweden) |
Albert Stadler (Switzerland) |
|
The solution:
It seems almost obvious that to obtain the minimum number of byes in a tournament we should have exactly one bye in any round with an odd number of contestants, and none in a round with an even number of contestants. On the other hand, because the number of byes in one round alters the number of contestants moving on to the next round, it seems possible that extra byes in one round might produce savings in a later round. To the contrary, using more than the minimum in any round strictly increases the total number of byes: Should round r have an even number c of contestants, the number of byes in that round, call it b, will also be even, and the number moving to round r + 1 will be
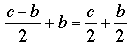 . Should c/2 and b/2 both be odd (which implies that b ≥ 2), then there would not have to be any byes in that round, representing a savings of at most one bye in round r + 1; but there were at least two extra byes in round r so there would be a net gain in the number of byes. Such an argument indicates that no matter what the policy is for the other rounds of the tournament, using more than b = 0 byes in round r would necessarily increase the number of byes in the tournament. A similar argument leads to the same conclusion when round r has an odd number of contestants (and, therefore, the number of byes would necessarily be odd). We will provide an alternative argument at the end, but for now let us agree that
. Should c/2 and b/2 both be odd (which implies that b ≥ 2), then there would not have to be any byes in that round, representing a savings of at most one bye in round r + 1; but there were at least two extra byes in round r so there would be a net gain in the number of byes. Such an argument indicates that no matter what the policy is for the other rounds of the tournament, using more than b = 0 byes in round r would necessarily increase the number of byes in the tournament. A similar argument leads to the same conclusion when round r has an odd number of contestants (and, therefore, the number of byes would necessarily be odd). We will provide an alternative argument at the end, but for now let us agree that
when there are c contestants in a round and c is even, then there will be no byes in that round and c/2 contestants will move to the next round; when c is odd then there will be 1 bye in that round, and (c + 1)/2 contestants will move on to the next round.
It follows that the minimum will be 3 byes when the knockout tournament begins with 2010 contestants; the number in each round will be
2010, 1005, 503, 252, 126, 63, 32, 16, 8, 4, 2.
We have emphasized the three rounds in which there must be a bye. Similarly, there will be 10 byes when the knockout tournament begins with 1025 contestants, one bye in every round until the last; the number of contestants in each round will be
1025, 513, 257, 129, 65, 33, 17, 9, 5, 3, 2.
Most of our correspondents noted a connection between the rule for counting the minimum number of byes and the algorithm for converting a base-10 number to binary. It turns out that the minimum number of byes in a tournament with n participants equals the number of zeros in the base-2 representation of the number n – 1. Dima and Robinson both provided a reference to the encyclopedia of integer sequences,
http://www.research.att.com/~njas/sequences/A080791.
Unfortunately, no explanation is provided on that web page. An even nicer way to compute this number is to let h be the least integer for which 2h ≥ n. Then
the minimum number of byes in a tournament with n participants equals the number of ones in the base-2 representation of the number 2h – n.
It is clear that these two rules produce the same result: 2h – 1 is a number whose base-2 representation consists of all ones, so that 2h – n = 2h – 1 – (n – 1) is a binary number that has a one in precisely those positions where (n – 1)2 has a zero. For example,
2010 – 1 = 2009 = 111110110012 has three 0s;
211 – 2010 = 2048 – 2010 = 38 = 1001102 has three 1s.
Kouba provided a few other simple examples:
| for n |
= 2k |
the number of byes is |
0, |
| |
= 2k – 1 |
|
1, |
| |
= 2k + 1 |
|
k. |
To show why this rule works we will combine the arguments sent in by Jakobsson and by Dumortier, with ideas from Baiocchi, Cairoli, and Kouba. We introduce the notion of an imaginary contestant (as opposed to an actual contestant) to bring the number in each round up to a power of 2. Of course, imaginary contestants play imaginary matches — the number of actual matches in a tournament with n contestants is always n – 1 (because everybody but the tournament champion must lose exactly one game). Recall that h is the least integer for which 2h ≥ n. We define
Cr to be the number of actual contestants in round r (so that C1 = n),
Ir = 2h–r+1 – Cr to be the number of imaginary contestants in round r,
Mr to be the number of actual matches that are played in round r,
IMr to be the number of matches imagined between two imaginary contestants,
Hr to be the number of hybrid matches (between a real and imaginary contestant).
Here are the numbers for the tournament with n = 2010 participants using the rule that at most one imaginary player can be paired with a real contestant in any round.
r |
Cr |
Ir |
Mr |
IMr |
Hr |
1 |
2010 |
38 |
1005 |
19 |
0 |
2 |
1005 |
19 |
502 |
9 |
1 |
3 |
503 |
9 |
251 |
4 |
1 |
4 |
252 |
4 |
126 |
2 |
0 |
5 |
126 |
2 |
63 |
1 |
0 |
6 |
63 |
1 |
31 |
0 |
1 |
7 |
32 |
0 |
16 |
0 |
0 |
8 |
16 |
0 |
8 |
0 |
0 |
9 |
8 |
0 |
4 |
0 |
0 |
10 |
4 |
0 |
2 |
0 |
0 |
11 |
2 |
0 |
1 |
0 |
0 |
In a hybrid match, we agree that the actual contestant moves to the next round and the imaginary is eliminated; that is, Hr represents the number of byes in round r. The number of contestants in the next round satisfies
Cr+1 = Hr + Mr.
This, then, is the alternative argument we promised earlier — to keep the total in the Hr column as small as possible, we schedule a hybrid match only when needed: The number of hybrid matches in each round equals the total number of other matches in that round (both actual and imaginary) subtracted from 2h–r (where 2h–r equals half the total number of actual and imaginary contestants in that round). Consequently, the number of matches Mr + IMr + Hr = 2h–r in each round: if Mr is decreased by k, then so is IMr and Hr goes up by 2k. Because the total in the Mr column will always be one less than the number of contestants, we get the least number of byes in a tournament by maximizing the number of imaginary matches; that is, we have Hr at most 1 for each r.
To fill in the above table, we began with C1 = 2010 and h = 11; thus, I1 = 211 – 2010 = 38. When Cr is even, we have the number of matches satisfies 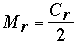 ; when Cr is odd,
; when Cr is odd, 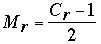 . In either case, Cr+1 = Cr – Mr (that is, one contestant is eliminated after each match). Analogous formulas hold for the imaginary contestants, whose number (by definition) has the same parity as Cr: IMr =
. In either case, Cr+1 = Cr – Mr (that is, one contestant is eliminated after each match). Analogous formulas hold for the imaginary contestants, whose number (by definition) has the same parity as Cr: IMr =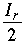 or
or 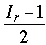
according as Ir is even or odd.
The table should make clear how the number of byes (which is the sum of the numbers in the Hr column) is related to the binary representation of I1 = 2h – C1. Indeed, the column headed Hr gives the digits of I1 in reverse order (starting with the units digit): 38 = 1001102. To determine the binary representation of 38, divide 2 into 38; this gives 19 pairs with no singleton left over, so that the remainder 0 is the units digit,
38 = 2·19 + 0.
Next, the 19 pairs divided by 2 equals 9 groups of two pairs plus a remainder of 1 (which means that there are 9 groupings of size 4 with one group of 2 left over), whence 1 is the two's digit,
19 = 2·9 + 1.
In general, Ir divided by 2 equals Ir+1 with a remainder of Hr, whence Hr is the digit in the 2r–1 position in the binary representation of I1:
9 = 2·4 + 1
4 = 2·2 + 0
2 = 2·1 + 0
1 = 2·0 + 1.
Further comment. It is not clear that there is any practical advantage is to running a tournament with the minimum number of byes. Most tournaments are arranged so that all the byes are in the first round. (In the colorful language we used above, when all byes are in the first round, every imaginary player is matched with an actual player in the first round, so that there are Ir hybrid matches in the first round, and none in any subsequent round.) In this way the organizers can control who gets the byes. Perhaps having the minimum number of byes is somewhat more equitable in that it minimizes the number of times contestants are matched who have played a different number of matches.
|

