|
Solution for April 2011
| The Problem: |
 |
- Does there exist a continuous real-valued function $f: \mathbb{ R}\rightarrow \mathbb{ R}\;$ that takes each of its values exactly twice?
- Does there exist a continuous real-valued function $f: \mathbb{ R}\rightarrow \mathbb{ R}\;$ that takes each of its values exactly three times?
Answer.
No for part (a); Yes for part (b).
|
Correct responses: |
 |
Correct solutions to the March problem were submitted by
| Lou Cairoli (USA) |
Mei-Hui Fang (Austria) |
| Philippe Fondanaiche (France) |
Gruian Cornel (Romania) |
| Tom Holens (Manitoba) |
Lars Huettenberger (Germany) |
| Benoît Humbert (France) |
Ile Ilijevski (Macedonia) |
| Kipp Johnson (USA) |
Omran Kouba (Syria) |
| Antek Łączkowski (Poland) |
Matthew Lim (USA) |
| Patrick J. LoPresti (USA) |
Fatemeh Naghipour (Regina) |
| Paolo Perfetti (Italy) |
Shpetim Rexhepi (Macedonia) |
| John T. Robinson (USA) |
Ignacio Somma Esteves |
| Albert Stadler (Switzerland) |
|
|
The solution:
Solution to part (a).
Preliminary comments. Our argument is based on two fundamental theorems about the real line:
The Intermediate Value Theorem. If $f(x)$ is a real-valued continuous function for $a \le x \le b$, and $r$ is any number between $f(a)$ and $f(b)$, then there is a number $c$ between $a$ and $b$ such that $f(c) = r$. (This theorem captures the intuitive notion that you can draw a continuous function without lifting your pencil off the paper.)
The Extreme Value Theorem. If $f(x)$ is a real-valued continuous function for $a \le x \le b$, then it must attain its maximum and minimum values on that interval. (In other words, there exist $c$ and $d$ in the in the closed interval from $a$ to $b$ such that $f(c) \ge f(x) \ge f(d)$ for all $x$ with $a \le x \le b$.)
For many centuries mathematicians used these theorems tacitly, thinking that they were obvious if they thought about them at all. It was only in the nineteenth century that they were carefully formulated and became part of the foundations of analysis. On the other hand, the properties do have intuitive appeal and should cause the reader no difficulty even if he has never seen them before. For further details see the relevant Wikipedia pages, or any calculus or analysis textbook. Perfetti spotted our problem as number $1.3.22$ on page 17 of Problems in Mathematical Analysis II, Continuity and erentiation, by W.J. Kaczor and M.T. Nowak, published by the American Mathematical Society (2001). All the submitted proofs were quite similar; our argument has been taken mostly from Patrick LoPresti, with additional ideas from the other submissions.
Nonexistence proof.
Suppose to the contrary that a function $f(x)$ were to exist that takes every value in its range exactly twice. Choose some number $r$ in its range; for convenience, let us take $r=0$. (The function $g(x) =f(x)-r$ would take each of its values exactly twice if and only if $f(x)$ does, so we could have started with $g$.) By hypothesis, then, $f(x)=0$ for exactly two values of $x$, say $a$ and $b$; that is, $f(a) = f(b) = 0$ and f is nonzero elsewhere.
Consider the behavior of $f(x)$ when $a<x<b$. Observe that $f(x)$ must be either entirely positive or entirely negative on this open interval, for if it were positive somewhere and negative somewhere else between $x=a$ and $x=b$, then by the Intermediate Value Theorem it would be zero somewhere in between, and that would be a third zero of $f(x)$, contrary to our hypothesis. Without loss of generality, suppose $f(x)$ is positive between $a$ and $b$. (Should it be negative, simply replace it by $-f(x)$.) Now, by the Extreme Value Theorem, f(x) attains its maximum value, call it $M$: $f(c) = M$ for some $c$ for which $a \le c \le b$. In fact, because $f(x)$ is zero at $a$ and $b$ and positive in between, $M$ must be positive, and thus $a < c < b$. By hypothesis, there is exactly one other value of $x$, say $x=d \ne c$, such that $f(x) = M$. Where can $d$ possibly be?
Suppose $d > b$. Then we have
$$a < c < b < d, \quad f(a) = 0, f(c) = M, f(b) =0, \mbox{ and } f(d) = M.$$
But by the Intermediate Value Theorem, $f(x)$ would necessarily assume every value from $0$ to $M$ as $x$ runs from $a$ to $c$, and again as $x$ runs from $c$ to $b$, and a third time for $x$ between $b$ and $d$. That is, $f(x)$ would necessarily assume each of its values at least three times, which is a contradiction. So $d$ cannot be greater than $b$. By similar reasoning, $d$ cannot be less than $a$. Certainly $d$ cannot equal $a$ or $b$ (because $f(d) = M$ is positive and $f(a) = f(b) = 0$). That leaves only the possibility that $d$ lies between $a$ and $b$. Suppose we have labeled them so that $c < d$. By definition, $M$ is the maximum value of $f(x)$ for $x$ between $a$ and $b$; in particular, between $x=c$ and $x=d$, $f(x) \le M$. But nowhere in that interval can $f(x)$ be equal to $M$ since $f(x)$ takes each of its values only twice. So $f(x)$ must be less than $M$ between $x=c$ and $x=d$. But that is likewise impossible: again by the Intermediate Value Theorem, $f(x)$ already takes on every positive value less than $M$ when $x$ is between $a$ and $c$, and a second time when $x$ is between $d$ and $b$, whence, by hypothesis, it cannot take any value less than $M$ for a third time. That eliminates all possible locations for $d$, and we conclude that it is not possible for $f(x)$ to take each of its values exactly twice.
Comment. Fang, Fondanaiche, Humbert, and LoPresti observed that, more generally, there can exist no continuous function that takes each of its values exactly $n$ times, if $n$ is an even number. A careful modification of our argument above will prove their claim.
Solution to part (b). Examples of continuous functions that take each of its values exactly times came in three varieties:
Type 1.
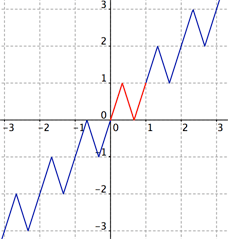 |
For each integer $k$ define
$$\small f(x) = \left\{
\begin{array}{lcc}
3(x-k) + k & 0 \le x-k \le \frac13 \\
-3(x-k)+2+k & \frac13 \le x-k \le \frac23 \\
3(x-k) -2+k & \frac23 \le x-k \le 1
\end{array}
\right ..$$ |
Figure 1: f(x)
Figure 1 is a slight modification of the GeoGebra file sent to us by Benoît Humbert. GeoGebra, as the name implies, combines graphics with algebra. The software can be downloaded for free, but it might take a while to figure out how to use it.
Type 2.
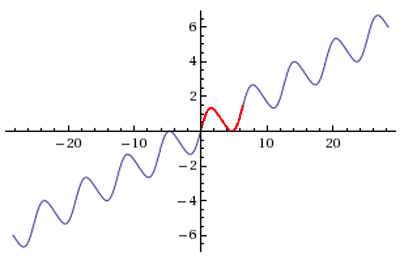
Figure 2: $g(x) = \frac2{3\pi}x + \sin x +\frac1{3\pi}\sin 2\pi$
Figure 2 is a copy of the WolframAlpha web page produced by Patrick LoPresti, which he obtained by typing
graph[2/(3pi)*x + sin(x) + 1/(3pi)*sin(2x)]
into the space provided on the page www.wolframalpha.com. You can explore the resulting figure there by moving your mouse around, and you can modify the equation at will.
Type 3.
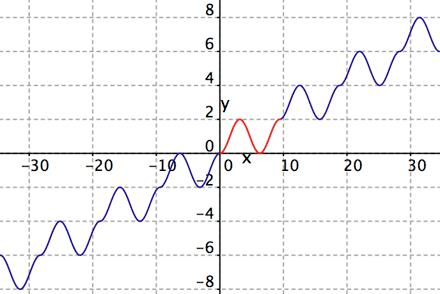
Figure 3: For each integer $k$ define
$h(x) = (2k+1)- (-1)^k\cos x$, for $3k\pi \le x \le 3(k+1)\pi$.
Each of the three pictures clearly shows a function that takes every real value exactly three times: Note that the relative extreme points of each curve are evenly spaced; consider a portion of the curve (such as the N-shaped path shown in red in Figure 1 from $(0, 0)$ to $(1,1)$) that begins half-way between a relative minimum and a relative maximum, includes two extreme points, then ends half-way to the next relative maximum. We can think of it as a fundamental unit that is repeated throughout the graph. That portion of each graph takes on each $y$-value except the first and last exactly three times; the initial $y$-value equals the the relative minimum on the right and the relative maximum of the previous fundamental unit, while the final $y$-value equals the maximum on the left and the minimum of the next fundamental unit. This intuitive discussion is easily confirmed by the functions that accompany the first and third figures (labeled $f$ and $h$). The second formula takes a bit more work to verify: You must show that the derivative of $g(x)$ is zero at all odd multiples of $\frac\pi2$, and that
$$g\left(\frac{(4k+1)\pi}2\right) = g\left(\frac{(4k+7)\pi}2\right)=\frac43(k+1) \mbox{ for all integers } k.$$
Further comments. It should be clear, more generally, that there exists a continuous real-valued function that takes every value of its range exactly $n$ times if and only if $n$ is odd. Indeed, for any odd natural number $n$ you can easily modify any of the three figures to produce continuous functions that take every real value exactly $n$ times — just draw $n-1$ points in each fundamental unit. In terms of algebra, the equation for $h(x)$ becomes
$$h_n(x) = (2k+1)- (-1)^k\cos x, \; \mbox{ for }\; nk\pi \le x \le n(k+1)\pi.$$
The case where $n=5$ is shown in Figure 4. Compare that curve with the general version of the function $g_n(x) = \frac2{n\pi}x + \sin x +\frac1{n\pi}\sin 2x$ shown in Figure 5 for $n=5$.
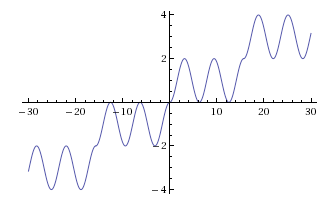
Figure 4: $h_5(x)$ takes every real value exactly five times.
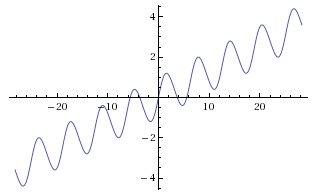
Figure 5: $g_5(x) = \frac2{5\pi}x + \sin x +\frac1{5\pi}\sin 2x$ takes every real value exactly five times.
It should likewise be clear that any open interval, finite or not, could serve as the range of a continuous function that takes each of its values exactly $n$ times when $n$ is odd: simply shrink the amplitude of each fundamental unit. When $n=3$ for example, to shrink the range of $h(x)$ to $-1< y < 1$, on each interval $3k\pi \le x \le 3(k+1)\pi$ for $k = 0, 1, 2, \dots$, define $h(x) = \frac{2^k-1}{2^k} + \frac1{2^{k+2}}(1- (-1)^k\cos x)$; extend the curve to the left by defining $h(-x) = -h(x)$. The right half of the function is shown in Figure 6.
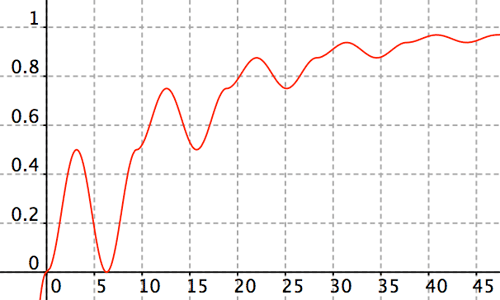
Figure 6: The range of $y=h(x)$ for $x\ge 0$ is $0 \le y < 1$.
|

