|
Solution for December 2010
| The Problem: |
 |
Is (20102011!)2 greater than 2010201120102011?

|
Correct responses: |
 |
Complete solutions to our December problem were submitted by
| Bojan Bašić (Serbia) |
Wolfgang Kais (Alemania) |
| Luigi Bernardini (Italy) |
Paul King (Ontario) |
| José Borges (Portugal) |
Normand LaLiberté (Ontario) |
| Lou Cairoli (USA) |
Matthew Lim (USA) |
| José David Calcines Padilla |
Remo Mantovanelli (Italy) |
| K.A. Chandrashekara (India) |
Nawal Kishor Mishra (India) |
| Bernard Collingnon (France) |
Vincent Pantaloni (France) |
| Gruian Cornel (Romania) |
Paolo Perfetti (Italy) |
| Shai Covo (Israel) |
Christian Pont (France) |
| Allen Druze (USA) |
Shpetim Rexhepi (Macedonia) |
| Mei-Hui Fang (Austria) |
John T. Robinson (USA) |
| Philippe Fondanaiche (France) |
Ilir Selmani (Macedonia) |
| Paul Führmann and Nicolas Michel (France) |
Heri Setiyawan (Indonesia) |
| Bruce Golfman (Austria) |
Madan Mohan Singhal |
| Verena Haider (Austria) |
Albert Stadler (Switzerland) |
| Paul Hatfield (Australia) |
Todd Stohs |
| Benoît Humbert (France) |
Damian Straszak (Poland) |
| Ile Ilijevski (Macedonia) |
A. Teitelman (Israel) |
| Kipp Johnson (USA) |
Paul Voyer (France) |
There were two incomplete submissions.
|
The solution:
The answer is yes; indeed, the contest is not even close. Bašić's computer determined that (20102011!)2 has more than 276 × 106 digits while 2010201120102011 has fewer than 147 × 106 digits — about half as many! Robinson observed that already when n = 3, (3!)2 > 33 (that is, 36 > 27), and he proved that (n!)2 grows faster than nn for n > 2. We received a splendid variety of proofs, with some correspondents sending us several arguments. The record came from D. Kipp Johnson who enjoyed the challenge so much, he sent us seven proofs! (His exact words were, "You’ve robbed me of too many hours of sleep on this one.") We will present four of his proofs, supplementing his work with a fifth proof from Singhal and Golfman, plus nice ideas from everybody else. The prize for simplicity goes to the first proof, while the prize for originality goes to the fifth.
Proof #1 An elementary inequality.
We first observe that for 1 ≤ k ≤ n,
k · (n - (k - 1)) = n + (k - 1)(n - k) ≥ n,
with equality when k = 1 or k = n, and a strict inequality when 1 < k < n. Thus for all integers n > 2,
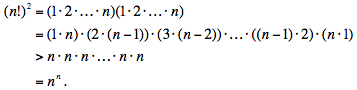
Proof # 2 Induction.
We claim that (n!)2 > nn for n ≥ 3.
By calculation we have (3!)2 = 36 and 33 = 27; thus (n!)2 > nn when n = 3. This is the base case. Now assume the claim for n = k; namely, (k!)2 > kk for some k ≥ 3. It is known (and we provide a simple proof in the next paragraph) that 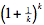 < 3 for all positive integers k, whence k + 1 > < 3 for all positive integers k, whence k + 1 > 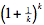 for k ≥ 2. Thus we have the following string of inequalities: for k ≥ 2. Thus we have the following string of inequalities:
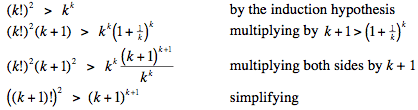
This completes the inductive step, and we conclude that the claim is true for all n ≥ 3; in particular, the claim is true for n = 20102011.
Comment. Because 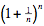 increases to the number e = 2.718... as increases to the number e = 2.718... as 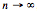 the sequence plays an important role in calculus. But you do not need calculus to prove the elementary claim that the sequence plays an important role in calculus. But you do not need calculus to prove the elementary claim that 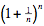 < 3, here is a simple argument sent to us by Verena Haider, which is based on the Binomial Theorem: < 3, here is a simple argument sent to us by Verena Haider, which is based on the Binomial Theorem:
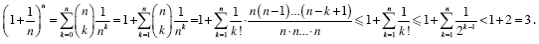
Proof #3 Stirling's Approximation.
The children's form of Stirling’s Approximation of n! states that 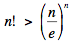 for all positive integers n; see MathWorld or Wikipedia for an easy proof using logarithms. When n ≥ 8 we have n > e2 , and we may write for all positive integers n; see MathWorld or Wikipedia for an easy proof using logarithms. When n ≥ 8 we have n > e2 , and we may write
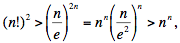
which establishes that (20102011!)2 > 2010201120102011.
Proof #4 Riemann Sum estimate of an integral. (We use Matthew Lim's version here.)
If n > e2, then ln n -2 > 0 and
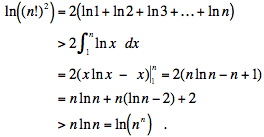
Finally, apply the exponential function to both sides of the equation to get (n!)2 > nn for all integers n ≥ 8.
Comment. This proof is essentially the same as Proof #3, except here we tacitly proved the elementary form of Stirling's formula without stating it.
As a bonus, here is one approach that Johnson seems to have overlooked. This argument came from Madan Mohan Singhal; Bruce Golfman provided a similar proof.
Proof #5 The arithmetic-geometric mean.
The sequence
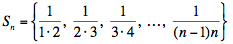
has n – 1 terms, which are distinct when n > 2. Its arithmetic mean is
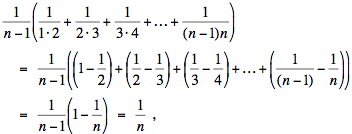
and its geometric mean is
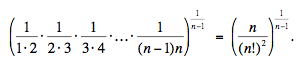
Because for sequences of distinct elements the arithmetic mean is always greater than the geometric mean, we deduce that for n > 2,
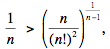
or
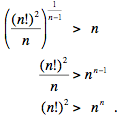
| 
