Solution for March 2011

The Problem:

This month's problem is our tribute to Jorge Luis Borges, the author of The Book of Sands and The Library of Babel. The Cabbalistic Encyclopedia of Permutations of the Roman Alphabet consists of seven volumes listing the permutations of the 26-letter Roman alphabet in alphabetical order.  The volumes are very large, and written in very small print, because there are many of these permutations.  Each volume contains exactly one-seventh of all permutations; if you open Volume 1 at the very first page and peer through your magnifying glass, you will see the first permutation abcdefghijklmnopqrstuvwxyz appearing at the top, followed immediately by abcdefghijklmnopqrstuvwxzy. Our problem: What is the very last permutation listed in this first volume? Answer. dswoeczyxvutrqpnmlkjihgfba.

Correct responses:

Correct solutions to the March problem were submitted by Luigi Bernardini (Italy) Daniel Bitin Lou Cairoli (USA) Bernard Collignon (France) Mei-Hui Fang (Austria) Philippe Fondanaiche (France) Gruian Cornel (Romania) Tom Holens (Manitoba) Benoît Humbert (France) Ile Ilijevski (Macedonia) Kipp Johnson (USA) Wolfgang Kais (Germany) Antek Łączkowski (Poland) Matthew Lim (USA) Patrick J. LoPresti (USA) M.C. Juan Mir Pieras (Spain) John T. Robinson (USA) Dustin Sawatzky Mathias Schenker (Switzerland) Albert Stadler (Switzerland) Hakan Summakoğlu (Turkey) Paul Voyer (France)

The solution:

Each volume contains exactly $\frac17 \times 26! = 26 \times 25 \times 24\times 23\times22\times3\times20!$ entries. Because 7 divides evenly into $\frac{26!}{20!}$, our task reduces to determining the first six letters of the final entry of the first volume: All $20!$ permutations beginning with those first six letters will appear together at the end of the first volume, and the final permutation that begins with those first six letters, which will be the final entry in volume 1, will have as its last 20 letters the remaining 20 letters of the alphabet in reverse alphabetical order.

Our solution comes down to the simple observation that the 26! permutations are arranged into 26 equal-sized blocks. The first block contains all 25! permutations that begin with the letter $a$; that block is followed by the 25! permutations beginning with $b$, and so on down to the 25! permutations beginning with $z$. (If this observation and its consequences are not obvious to the reader, he should try, as a preliminary exercise, arranging alphabetically the $4! = 24$ permutations of the letters $abcd$ into three columns, each with eight entries.) The first volume contains $1/7$ of those blocks: Because $\frac{26}7 = 3 + \frac57$, it contains the entire blocks that begin with the letters $a, b$, and $c$, and $\frac57$ of the block beginning with $d$.

The 25! permutations beginning with $d$ are arranged in blocks of size $24!$, each beginning with a letter other than $d$. Because $\frac57 \times 25 = 17 + \frac67$, the final block of the first volume begins with the

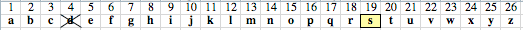
18th letter of the alphabet with $d$ removed, namely $s$. We therefore will find
our third letter $\frac67$ of the way down the list of permutations beginning with $ds$. The pattern should now be clear: we are expanding the fraction $\frac{26!}{7}$ in the peculiar way,
$$\frac{26!}7 = 3\cdot 25! + 17\cdot 24! + 20 \cdot 23! + 13\cdot22!+3\cdot21! + 3\cdot 20!,$$
which is explained by the following table: 

\[ \begin{array}{lll} \frac 47 \cdot 23 = 13 + \frac 17 & \quad \frac 17 \cdot 22 = 3 + \frac17 & \quad \frac17 \cdot 21 = 3 \\ \frac 47 \cdot 23 = 13 + \frac 17 & \quad \frac 17 \cdot 22 = 3 + \frac17 &\quad \frac17 \cdot 21 = 3\end{array}\]

In particular, after determining that that first two letters of our target permutation are $ds$, we go $20\cdot23!$ permutations down the list and see that the third letter will be the $20 + 1 = 21$st among the remaining letters, namely $w$, with the remaining string of letters being abcefghijklmnopqrtuvxyz. Then $13\cdot22!$ more permutations to determine that the fourth letter is the $14$th of the remaining $23$ letters, namely $o$. Then $3\cdot 21!$ more permutations to find the fifth letter is four letters down, namely $e$, followed by $3\cdot 20!$ permutations to find that the sixth letter is $f$. The remaining string of letters is abcghijklmnpqrtuvxyz; as mentioned above, these come at the very end of the portion of all permutations that begin dswoef, so these final 20 letters will appear in reverse alphabetical order.

Comments. Several solvers noted how the solution to our permutation problem recalls the process of converting a number from base 10 to another base. Indeed, every positive integer less than $(n+1)!$ has a unique representation
$$a_nn! + a_{n-1}(n-1)! + \dots + a_1(1!) + a_0(0!)\;,$$
where $a_k$ is an integer, $0 \le a_k \le k$ for all $k = 0, \dots , n$. This number can be denoted
$$a_na_{n-1}\dots a_10_!,$$
with the factorial subscript suggesting the relationship of this factorial representation to a representation in a fixed base. So, for example, $13 = 2010_! = 2\cdot3! + 0\cdot 2! + 1\cdot 1! + 0 \cdot 0!$, while the permutation of our problem --- the final permutation of volume 1 --- would appear as permutation number $3[17][20][13]3300\dots0_!$, which ends in $20$ zeros (and the brackets indicate that the numbers enclosed by them are to be considered single digits).
Details can be found in a Wikipedia article, among other places:
http://en.wikipedia.org/wiki/Factorial_number_system. Several correspondents devised their own computer programs to convert the factorial number into the corresponding permutation. Both Schenker and Kais listed the first and last permutation of each volume. We include the list here so that the reader can test his own algorithm.

\[ \begin{array}{ccc}
\hline
% after \\ : \hline or \cline{col1-col2} \cline{col3-col4} ...
\mbox{Volume} & \mbox{First Permutation} & \mbox{Last Permutation} \\
\hline
1 & \mbox{abcdefghijklmnopqrstuvwxyz} &\mbox{dswoeczyxvutrqpnmlkjihgfba} \\
2 & \mbox{dswoefabcghijklmnpqrtuvxyz} &\mbox{hltdigzyxwvusrqponmkjfecba}\\
3 & \mbox{hltdijabcefgkmnopqrsuvwxyz} &\mbox{ldptkjzyxwvusrqonmihgfecba}\\
4 & \mbox{ldptkmabcefghijnoqrsuvwxyz} &\mbox{owkgpnzyxvutsrqmljihfedcba}\\
5 & \mbox{owkgpqabcdefhijlmnrstuvxyz} &\mbox{sogwrqzyxvutpnmlkjihfedcba}\\
6 & \mbox{sogwrtabcdefhijklmnpquvxyz} &\mbox{whdlvuzyxtsrqponmkjigfecba}\\
7 & \mbox{whdlvxabcefgijkmnopqrstuyz} &\mbox{zyxwvutsrqponmlkjihgfedcba}\\
\hline
\end{array} \]

Lou Cairoli came across a nice recreational math book related to this month's problem, which we pass along: William Goldbloom Block, The Unimaginable Mathematics of Borges’ Library of Babel, Oxford University Press, 2008.

Kipp Johnson provided the easiest solution to the March problem: he ordered the Cabbalistic Encyclopedia from amazon.com and turned to the last page. It is somewhat vexing to learn, however, that the Encyclopedia is no longer in print while books like Webster's Dictionary seem to be selling well even though they contain vastly fewer words and even allow repetition of letters. Speaking of vexing,
Albert Stadler found the permutations

• Blowzy night-frumps vex'd Jack Q. and
  
  
• Glum Schwartzkopf vex'd by NJ IQ.

in the Encyclopedia. He reported that each volume of his copy has exactly one million pages, and he challenges the reader to determine the pages on which these permutations appear. (Send your guesses to him, not to us!) Meanwhile Cairoli reported that sentences using all letters of the alphabet are called pangrams (or holoalphabetic sentences, if you are sufficiently pretentious), and offered permutation number 196307974427380973351813573 as a minimal example, namely

Mr. Jock, TV quiz PhD, bags few lynx.

On the other hand, nobody seems to have noticed that DSWOEC is, in fact, an acronym that stands for Don't Squander Words On Esoteric Comments.

Since Cairoli was not able to find a copy of the encyclopedia, he wondered about the size of the volumes. There are about $4.03 \times 10^{26}$ permutations in the text, a number that is not only larger than the current US national debt, but it exceeds published estimates for the number of grains of sand on earth (fewer that $10^{24}$ according to http://www.newton.dep.anl.gov/askasci/ast99/ast99215.htm, but the web page fails to say who counted them). He estimated that it would have taken a million fanatical monks, each writing a permutation per second, over 2 billion years to complete the task.