Solution for May 2011

The Problem:

A connect-the-dots puzzle is a collection of $n$ distinct points in the plane numbered from $1$ to $n$ such that no line contains three consecutive points $i, i+1, i+2$ (or $n-1, n, 1$). Our problem this month comes in two parts. Show that for every $n>13$ you can produce a connect-the-dots puzzle with $n$ points such that every line of the plane that contains a pair of consecutive points will contain at least one other pair of consecutive points. Show that for any 13-point puzzle there exists a straight line that contains one and only one pair of consecutive points.

The solution:

Our solutions this month came from Philippe Fondanaiche (France), Gruian Cornel (Romania), Benoît Humbert (France), John T. Robinson (USA), and Paul Voyer (France). The problem is based on Problem 70 from Crux Mathematicorum 1 (Dec. 1975) page 102, back in the days when the journal was called Eureka. We speculated that the problem had attracted few solvers thirty-six years ago because it had not been clearly stated; however, few of our regular correspondents submitted a solution this month, so maybe there is a problem with the problem. Indeed, Humbert noted that contrary to the claim in part (b) (before we added the requirement that the 13 points be distinct), you could have a 13-point puzzle that satisfied all of our conditions by allowing some segments joining consecutive points to overlap. Here is the example he provided.

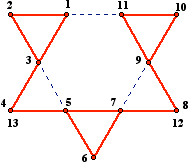
Figure 1: Humbert's counterexample with 13 points.

Consequently, for (b) to hold we have now required the points of the puzzle to be distinct.

Solution to part (a). For all $n \ge 10$ except for $n=11$ and $13$, we present a composite of the constructions devised by Fondanaiche and by Gruian. For even values of $n$, say $n=2k$ with $k \ge 5$, we label the vertices of a regular convex $k$-gon $A_1, A_2, \dots, A_k$ (as on the left side of Figures 2 and 3, where $k = 6$ and $7$).

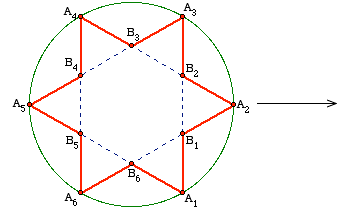
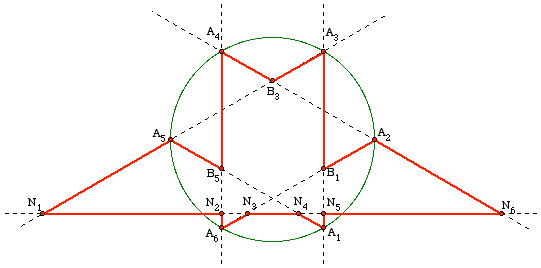
Figure 2: Puzzle with 12 points and the derived version with 15 points.

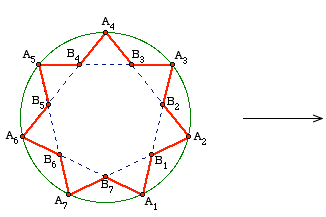
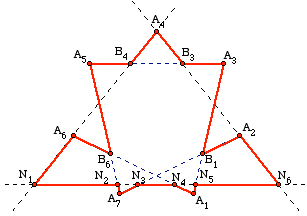
Figure 3: Puzzle with 14 points and the derived version with 17 points.

We use the letter $B$ to label the points where the shortest diagonals intersect, so that $A_1A_3$ intersects $A_kA_2$ at $B_1$, $A_2A_4$ intersects $A_1A_3$ at $B_2$, and in general,
$$B_i = A_iA_{i+2} \cap A_{i-1}A_{i+1}.$$
Now number the points $A_1,B_1,A_2,B_2,A_3,B_3,\dots B_k$ in this order starting at 1 (so that $A_i$ gets numbered $2i-1$ and $B_i$ gets numbered $2i$). Join $A_i$ to $B_i$ and $B_i$ to $A_{i+1}$ to get the zigzag path shown in red on the left in the above figures. Note that each of the $k$ diagonals contains a pair of red segments (namely $A_iB_i$ and $B_{i+1}A_{i+2}$), and so we have produced a puzzle with $n=2k$ distinct points for every even number $n \ge 10$ such that every line of the plane that contains a pair of consecutive points contains a second pair of consecutive points.

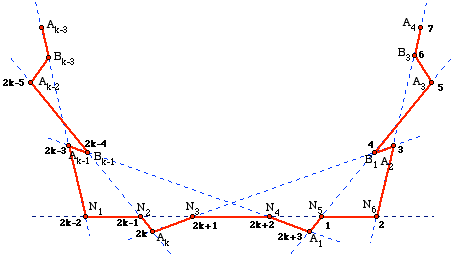
Figure 4: The derivation of a puzzle with $2k+3$ points from one with $2k$ points.

We now show how to modify a puzzle that has $2k$ points to produce a puzzle with $2k+3$ points when $k \ge 6$, which will provide the desired examples of puzzles with an odd number of points. As illustrated in Figure 4 (and on the right side of Figures 2 and 3), in our puzzle that starts with a regular $k$-gon we let $\ell$ be the line joining the midpoints of the segments $A_kB_k$ and $B_kA_1$. Delete the points $B_k, B_2$, and $B_{k-2}$ and label by $N_1$ to $N_6$ the six new points where $\ell$ intersects six consecutive diagonals as in Figures 2 through 4:
$$N_1 \mbox { on } A_{k-3}A_{k-1}, N_2 \mbox { on } A_{k-2}A_{k}, N_3 \mbox { on } A_{k}A_{2},$$

$$N_4 \mbox { on } A_{k-1}A_{1}, N_5 \mbox { on } A_{1}A_{3}, N_6 \mbox { on } A_{2}A_{4}.$$
The points of our puzzle will be numbered as before from the 5th point $A_3$ to the $(2k-5)$th point $A_{k-2}$, but the numbering now begins with $N_5$ as our first point:
$$N_5,N_6,A_2,B_1,A_3$$
are the points numbered 1 to 5, while the final points are
$$A_{k-2},B_{k-1},A_{k-1},N_1,N_2,A_k,N_3,N_4,A_1,N_5,$$
which get the numbers $2k-5,2k-4,2k-3,2k-2, 2k-1, 2k, 2k+1, 2k+2, 2k+3, 1$. Note that the new puzzle now has $2k - 3 + 6 = 2k+3$ points; moreover, each of the unmodified diagonals of the original $k$-gon continues to contain a pair of segments (namely $A_iB_i$ and $B_{i+1}A_{i+2}$), while the six modified diagonals each has one new point $N_i$ in place of one of the $B$'s, and the new line $\ell$ contains three segments (namely $N_1N_2, N_3N_4, N_5N_6$). This provides a solution to part (a) of our problem for all odd numbers $n \ge 15$.

Solution to part (b). We received two types of arguments to deal with part (b), but we should first make clear what we are to prove. We shall use the word segment to refer to the line segment that joins a pair of consecutive points of a puzzle, and we call a line of the plane a support line if it contains one or more of those segments.

Restatement of part (b). No 13-point connect-the-dots puzzle can satisfy all of the following three properties:

1. each point of the puzzle belongs to two and only two segments,
   
   
2. no support line contains three consecutive points of the puzzle, and
   
   
3. all support lines contain two or more segments.

Proof 1. Assume to the contrary that there exists a 13-point puzzle that satisfies all three properties. Of course, the puzzle would have 13 segments. It follows from (iii) that there can be at most six support lines. Each of those six lines would intersect the other five support lines in at most five points; therefore the number of segments per line cannot be more than 2 (since each segment has two endpoints while properties (i) and (ii) imply that segments on the same support line must have disjoint end points). But then there can be at most $6 \times 2 = 12$ points in the puzzle; that is, there cannot have been 13 points to start with. Comment. Note that a similar argument shows that an 11-point puzzle will likewise necessarily have at least one support line containing only one segment — a puzzle with an odd number of points in which every support line contains at least two segments will necessarily have a support line with three segments, which requires at least 15 points. We will see this more clearly with our second argument.

Proof 2. Here we prove that any connect-the-dots puzzle with an odd number of points that satisfies all three properties must have at least $15$ points. If there are exactly two segments on every support line, the number of points in the puzzle would be even by properties (i) and (ii). Since we assume here that the number of points is odd, property (iii) implies that at least one support line, call it $\ell$, will contain three segments, which have disjoint end points by (i) and (ii). Through each of the six end points of those segments there would be at least one other support line, and on each of those six or more support lines there would be at least three further points of the puzzle. Because (by (i) and (ii)) each of those further points would be on two support lines different from $\ell$, that would account for at least $\frac{6 \times 3}{2} = 9$ points. Those 9 points plus the 6 on $\ell$ total at least 15 points, as claimed. Comment. A similar argument shows that a puzzle with an even number of points would necessarily have at least $\frac{4 \times 3}{2} + 4= 10$ points.