|
Solution for November 2010
| The Problem: |
 |
Compute
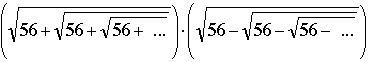
and justify your answer.
|
Correct responses: |
 |
All our correspondents found a way to get the right answer, but those who have dealt with infinite series before realized that there was a subtle point that they had to address. We have separated the list of solvers into two parts -- those who submitted a complete solution and those who provided only an answer.
Complete solutions to our November problem were submitted by
Bojan Bašić
(Serbia) |
Verena Haider
(Austria) |
Matthew Lim
(USA) |
José Borges
(Portugal) |
Benoît Humbert
(France) |
Alex Love
(Ontario) |
Shai Covo
(Israel) |
Kipp Johnson
(USA) |
Christian Pont
(France) |
Mei-Hui Fang
(Austria) |
Wolfgang Kais
(Germany) |
John T. Robinson
(USA) |
Philippe Fondanaiche
(France) |
Normand Laliberté
(Ontario) |
Albert Stadler
(Switzerland) |
Bruce Golfman
(Austria) |
Marc Lichtenberg
(France) |
Damian Straszak
(Poland) |
Correct answers to our November problem were submitted by
Mehdi Abdeh-Kolahchi
(Canada) |
Cornel Gruian
(Romania) |
Milan Pavic
(Serbia) |
Christopher Abdnour
(USA) |
Tom Holens
(Manitoba) |
Anonymous |
Luigi Bernardini
(Italy) |
Ile Ilijevski
(Macedonia) |
Raffaele Rainone
(Italy) |
Daniel Bitin
|
Hasan Kolcu
(UK) |
Shpetim Rexhepi
(Macedonia) |
K.A. Chandrashekara
(India) |
Karim Laaouini
(Marocco) |
Francisco Suñol Esquirol
(Spain) |
Bernard Collignon
(France) |
Antonio Ledesma Lopez
(Spain) |
Mohammad Ali Syed
|
Allen Druze
(USA) |
Farid Lian
(Colombia) |
A. Teitelman
(Israel) |
Sébastien Dumortier
(France) |
Pavan Manjunath
(India) |
Paul Voyer
(France) |
Amit Elazari
|
Remo Mantovanelli
(Italy) |
Lasse Wollatz
(Germany) |
Sergey Gleizer
(USA) |
|
|
Our discussion is arranged in three parts: we first show how to get the answer, then we describe the subtlety, and finally we resolve remaining issues.
|
The solution:
Answer. Let  . Because x is defined by means of infinitely many square roots, it is not obvious that it represents a real number; however, should it be real then it would certainly be positive (because the square root symbol stands for the positive square root), and it would satisfy . Because x is defined by means of infinitely many square roots, it is not obvious that it represents a real number; however, should it be real then it would certainly be positive (because the square root symbol stands for the positive square root), and it would satisfy

That is, 0 = x2 - x - 56 = (x - 8)*(x + 7), so that x would necessarily equal 8. In the same way, letting y = 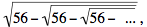
should y represent a real number then it would be the positive number that satisfies

so that y2 + y - 56 = (y - 7)(y + 8), whence y = 7. Combining these two calculations, we deduce that if both x and y are real numbers, then
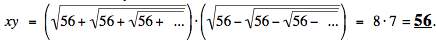
The subtle point. One must always proceed with caution when dealing with infinity. Both x and y were defined using an infinite sequence of square roots. These repeated roots are called nested radicals on the web pages both of Wikipedia and of MathWorld, to which you can turn for further information. (These radicals are variously called iterated or infinite in other reference works.) Nested radicals arise naturally; for example, the half-angle formula 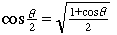 leads to the sequence of numbers leads to the sequence of numbers
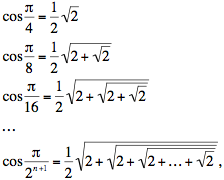
where the number of 2s under the radicals in the last expression is n. Infinite nested radicals probably first appeared in 1593 with Viète's remarkable formula for the constant : :
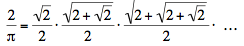 . .
Our x is defined to be the limit of the sequence
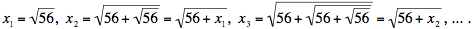 In general, In general, 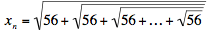 with the number 56 appearing n times, so that with the number 56 appearing n times, so that
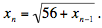 . .
Similarly, y is the limit of the sequence defined by
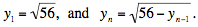 . .
It is not at all obvious that objects defined by means of infinite sequences should behave like real numbers and obey the arithmetic rules we learned in school. For an example of what might go wrong, consider the infinite sum
S = 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + ... .
Should this represent a real number, then we would have
S = 1 – ( 1 – 1 + 1 – 1 + 1 – 1 + 1 –...) = 1 – S,
whence 2S = 1, and S = ½. But one can argue that
S = (1 – 1) + (1 – 1) + (1 – 1) + (1 – 1) + ... = 0 + 0 + ... = 0.
Of course, you could just as easily obtain
S = 1 – (1 – 1) – (1 – 1) – (1 – 1) – ... = 1 – 0 – 0 – ... = 1.
So, what is going on? Does S = 0 or ½ or 1, or maybe somthing else? We try to make sense of an infinite sum by defining it to be the limit of an infinite sequence of finite sums,
S1 = 1, S2 = 1 - 1 = 0, S3 = 1 - 1 + 1 = 1, S4 = 1 - 1 + 1 - 1 = 0,... .
We see that this sequence alternates between the values 0 and 1, and does not approach a single real number that we could call its limit. We classify this sequence with the label divergent and set it aside for special treatment in advanced math courses. On the other hand, when you can show that some sequence eventually stays "arbitrarily close" to a real number, then you can apply the familiar arithmetic rules to it without any further concern. Returning to our November problem, we must now show that our two sequences both converge, xn to 8 and yn to 7. We received a variety of convergence proofs, from which we have selected three.
Proofs of convergence.
Proof 1. A composite of the proofs submitted by Borges and by Kais.
We already know that if the sequence
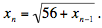 of nested radicals converges, it must converge to 8; it is sufficient, therefore, to prove that the sequence of nested radicals converges, it must converge to 8; it is sufficient, therefore, to prove that the sequence
{8 – xn} goes to zero:
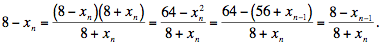
We are interested in the distance from xn to 8, so take the absolute value of both sides (noting that 8 + xn is always positive) to deduce that
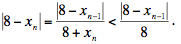
Repeat the calculation with n – 1 in place of n, then with n – 2, and so on down to |8 - x1| = |8 - √56| to get
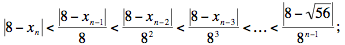
the term on the right goes to zero, which proves that xn approaches arbitrarily close to 8 as n goes to infinity.
Of course, the analogous argument shows that
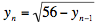 converges to 7: converges to 7:
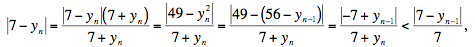
whence,
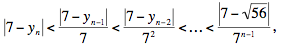
which also converges to zero as n goes to infinity. Our proof is complete.
A variation on the preceding argument was supplied by Haider and by Bašić, who used induction to establish the bounds
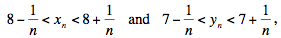
which shows easily that {xn} and {yn} converge to the appropriate limits as n goes to infinity.
Proof 2. A summary of the similar proofs submitted by Covo, Fang, Johnson, Humbert and Love.
A simple induction establishes that for all n, xn < 8; moreover, xn+1 > xn. Thus {xn} is an increasing sequence that is bounded above by 8, which implies that it has a limit. (One then shows that the limit is 8.) The sequence {yn} is somewhat harder to work with because yn > 7 when n is odd while yn < 7 when n is even (as can been seen in Proof 1 above). In other words, one must show that the odd terms decrease to the same limit that the even terms increase to. All five of the submitted proofs used straightforward calculations for this final step. Instead of reproducing one of those calculations, we will move on to the third approach.
Proof 3. A composite of the similar proofs that use calculus, submitted by Golfman, Pont, Stadler, and Straszak.
Here we change the role of x to that of a variable and consider the two functions
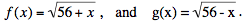
The iterative method of numerical analysis provides an easy way to solve appropriate equations of the form f(x) = x: if in the neighborhood of the solution the function has a derivative whose absolute value is less than some positive constant that is less than 1, and x0 is taken within that neighborhood, then the sequence {xn} defined by xn = f(xn–1) will converge to that solution. Note that the two sequences that came from our nested radicals can be defined by plugging x0 = 0 into the equation f(x) = x, and y0 = 0 into the equation g(x) = x:
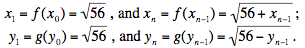
All we have to do is to investigate their derivatives:
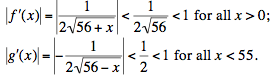
The desired conditions are satisfied for both functions, so we are assured that the corresponding sequences converge.
Further comments. Many of our correspondents remarked that 56 could be replaced by any real number r with r > 1:
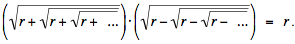
Moreover, in a recent article Javier Peralta ["On Some Infinite Sums of Iterated Radicals", International Journal of Mathematical Education in Science and Technology, 40:2 (March 2009) 290-300] claims to prove (but his proof seems to be missing a key step) that for r > 1,
 is an integer k if and only if r = k(k – 1),
is an integer k if and only if r = k(k – 1),
while
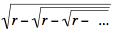 is an integer k if and only if r = k(k + 1). is an integer k if and only if r = k(k + 1).
Any of the methods discussed here would lead to a proof of Peralta's assertion.
|

