|
Solution for September 2012
| The Problem: |
 |
$N$ is a set containing some of the counting numbers from 1 to 15; it has the property that the product of any three of its numbers is not a square. For example, if $N$ were to contain 2 and 6, then it could not contain 12 because $2\cdot 6 \cdot 12 = 144$, which is a square. How large can $N$ possibly be?
|
The solution:
$N$ can contain at most 10 numbers.
Correct solutions were submitted by
Lamis Alsheikh (Syria) |
Aleksandar Blazhevski (Macedonia) |
Claudio Baiocchi (Italy) |
Bernard Collignon (France) |
Lou Cairoli (USA) |
Mei-Hui Fang (Austria) |
Philippe Fondanaiche (France) |
Tom Fuzesy (Regina) |
Benoît Humbert (France) |
Matthew Lim (USA) |
Mathias Schenker (Switzerland) |
Albert Stadler (Switzerland) |
| Hakan Summakoğlu (Turkey) |
Arthur Vause (UK) |
We also received three incorrect submissions.
Our problem this month is one of the number theory problems that made the short list for the 35th IMO, held in Hong Kong in 1994. Although the problem has a solution that is short and neat, it takes a long time to find any satisfactory solution, and many attempts that look promising tend to go astray; these aspects, perhaps, make the problem unsuitable for an Olympiad. In fact, most of the submitted solutions omitted details or made use of a computer. We received only four complete solutions. We present Lim's solution which is straightforward and easily understood, but requires lots of work. We follow that by Summakoğlu's solution which is elegant, but unmotivated if you haven't first taken a quick look at Lim's argument. The solutions from Fang and from Humbert are also quite nice; they are similar to the Olympiad committee's solution that can be found on various web sites such as
http://mks.mff.cuni.cz/kalva/short/soln/sh94n1.html.
Lim's solution with contributions from others.
The set of integers from 1 to 15, which we will call $S$, contains $15 \choose 3$ $= 455$ subsets of size 3; of these, just 18 consist of three integers whose product is a perfect square. We shall call them square triplets. It is quite easy to make a systematic list of all eighteen square triplets:
| {1,2,8} |
{2,3,6} |
{3,4,12} |
{5,8,10} |
| {1,3,12} |
{2,4,8} |
{3,5,15} |
{5,12,15} |
| {1,4,9} |
{2,5,10} |
{3,6,8} |
{6,8,12} |
| |
{2,6,12} |
{3,9,12} |
{6,10,15} |
| |
{2,7,14} |
|
{7,8,14} |
| |
{2,8,9} |
|
|
Our task is to find a subset $N$ of $S$ that is as large as possible while containing no subset in the list of square triplets; equivalently, we seek a set of numbers to omit from $N$ that is as small as possible yet intersects every square triplet. It is easy to verify that $X = \{1,2,8,12,15\}$ is a 5-element set that intersects each triplet; its complement $S-X = \{3,4,5,6,7,9,10,11,13,14\}$ is therefore a 10-element subset of $S$ with the desired property (that the product of any three of its numbers is not a square). But can we find an 11-element set satisfying that property? In other words, can we find a 4-element intersecting set? Before addressing that question, let's look at the list of all six 5-element intersecting sets; the list was found and verified via computer by several correspondents. One can check by hand that each of these sets contain at least one number in each of the 18 square triplets.
| {1,2,3,8,15} |
{1,2,8,12,15} |
{2,3,4,8,15} |
| {2,3,8,9,15} |
{2,4,8,12,15} |
{2,8,9,12,15} |
It follows that there are six subsets of size 10 in $S$ that would serve as candidates for the largest $N$.
We shall now see that any intersecting set must have at least 5 elements. Consider the following four disjoint square triplets:
$$\{1,4,9\}, \{2,3,6\}, \{5,12,15\}, \{7,8,14\}.$$
Because they are disjoint, we can be certain that any intersecting set will contain at least one number from each of these four sets. Note that this immediately implies that $N$ can contain no more that 11 numbers. What if we try to construct $N$ by removing 1 from the first set, 3 from the second, 5 from the third, and 7 from the fourth? Then the square triplet $\{2, 4, 8\}$ would remain as a subset of $N$, so the resulting 11-element candidate would not have the property we seek. There are, of course, $3^4 = 81$ ways to remove a single number from each of the four triplets; unless we can think of a short cut, we must find for all 81 possibilities a square triplet that remains in $N$ after those four numbers are removed, thereby forcing $N$ to exclude at least one more item. So pour yourself a drink, turn on the TV, sit back and make a list of the 81 ways to select the four items, and then in each case find a square triplet that has not been intersected. Happily, Lim has done the job for us:
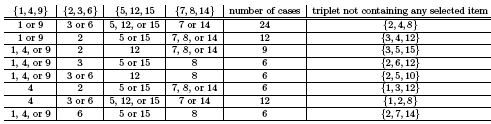
Thus, to exclude all square triplets $N$ must exclude more than 4 numbers from $S$, implying that $N$ has fewer than 11 numbers. Because we have an example where $N$ has 10 numbers, we see that the maximal size of $N$ is 10.
Summakoğlu's solution. We show that $N$ cannot be larger than 10 by proving that every set that intersects all square triplets must contain 5 or more numbers. It suffices to determine whether or not 2 or 3 is in the intersecting set. There are three possibilities to consider: (i) both 2 and 3 are in the intersecting set (and therefore not in $N$), (ii) 2 is in the intersecting set while 3 is in $N$, and (iii) 2 is in $N$.
Case ($i$). $2\not\in N$ and $3\not\in N$.
Because the three square triplets $\{1,4,9\}, \{5,12,15\}$, and $\{7,8,14\}$ are disjoint, at least one number from each of them must be omitted from $N$; therefore the resulting intersecting set will contain at least 5 numbers.
Case($ii$). $2\not\in N$ and $3\in N$.
Because we have $3 \in N$, at least one number from each of $\{5, 15\}$ and $\{6,8\}$ must be omitted from $N$; furthermore, because $\{3,1,12\}, \{3,4,12\}, \{3,9,12\}$, and $\{1,4,9\}$ are square triplets, either 12 together with one of 1, 4, or 9 are omitted, or we have both 3 and 12 in $N$ so that all three of 1, 4, and 9 must be omitted. Either way, the intersecting set will necessarily contain at least 5 numbers.
Case ($iii$). $2\in N$.
Because we have $2 \in N$, at least one number from each of $\{3, 6\}, \{5,10\}$ and $\{7,14\}$ must be omitted from $N$; furthermore, because $\{2,1,8\}, \{2,4,8\}, \{2,9,8\}$, and $\{1,4,9\}$ are square triplets, either 8 together with one of 1, 4, or 9 are omitted, or we have both 2 and 8 in $N$ so that all three of 1, 4, and 9 must be omitted. Either way, the intersecting set will necessarily contain at least 5 numbers.
We see that in every possible case, the intersecting set will contain at least 5 numbers; we conclude that $N$ can have at most 10 numbers.
|

