|
Solution for September 2009
| The Problem: |
 |
MP88 September 2009
The function f(x) satisfies two properties:
(i) f(x + y) + f(x - y) = 2[f(x) + f(y)], and
(ii) f(1) = 1.
What is f(22/7) ?
|
Correct responses: |
 |
Correct solutions were submitted this month by
Berkay Anahtarci (Turkey) |
Cornel Gruian (Romania) |
Roopesh Mangal (India) |
Claudio Baiocchi, (Italy) |
Omran Kouba (Syria) |
Patrick LoPresti (USA) |
Bojan Basic (Serbia) |
Gustavo Krimker (Regina) |
Milan Pavic (Serbia) |
Lou Cairoli (USA) |
Karim Laaouini (Morocco) |
Anonymous |
Bernard Collignon (France) |
Normand LaLiberté (Ontario) |
Mark Pilloff (USA) |
Olivier Cyr (France) |
Jinzhong Li (China) |
Aditya Prasad |
Allen Druze (USA) |
Matthew Lim (USA) |
John T. Robinson (USA) |
Federico Felizzi (Italy) |
Jeff Lindstrom (Ontario) |
Nutheti Shivdeep |
Bruce Gilligan (Regina) |
Jigang Luo (Regina) |
A. Teitelman (Israel) |
Philippe Fondanaiche
(France) |
José António
Nunes Borges (Portugal) |
Albert Stadler
(Switzerland) |
| Bernard Carpentier (France) |
|
|
In addition there were two correct solutions that were incomplete and one incorrect submission.
|
The solution:
It is easy to guess that the answer is
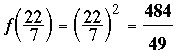 .
One way to start is by using the given properties to determine the value of f(x) for small values of x: .
One way to start is by using the given properties to determine the value of f(x) for small values of x:
If x = y = 0 then f(0) + f(0) = 2[f(0) + f(0)], so 2f(0) = 4f(0), whence f(0) = 0.
If x = y = 1 then f(2) + f(0) = 2[f(1) + f(1)] = 4, whence f(2) = 4.
If x = 2 and y = 1 then f(3) + f(1) = 2[f(2) + f(1)]; using our previous values of f this says that f(3) + 1 = 2[4 + 1], or f(3) = 9.
A pattern is starting to emerge! Most correspondents either used that pattern to obtain the answer directly (using nothing more than basic arithmetic), or they used induction to obtain a more general result. We present both methods.
The direct approach. We present here a composite of the solutions from Li, from Luo, and from Pavic. We have already seen that f(0) = 0. For any real number x, if we set y = x in (i) we get f(2x) + f(0) = 2(f(x) + f(x)) = 4 f(x), whence
f(2x) = 4 f(x).
It follows that 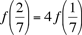 and and 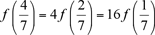 . .
With x = 2/7 and y = 1/7, we deduce that 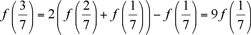 ; ;
thus, with x = 4/7 and y = 3/7, we deduce that
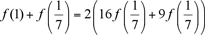 , so that , so that 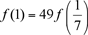 , and therefore, , and therefore,
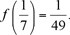
Next, using x = 1 and y = 4/7, we deduce that 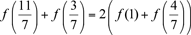 so that so that
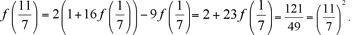
Finally, we use the doubling property to obtain
as claimed.
Mathematical induction. This is the approach taken by almost everybody else; we combine their proofs that for any real number r and integers m and n, n ≠ 0, conditions (i) and (ii) imply that
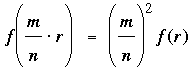
We first use induction to prove that f(m·r) = m2 f(r) for positive integers m:
We have already seen that f(0·r) = 0 = 02r, and trivially, f(1·r) = 12f(r). Assuming that f(k·r) = k2f(r) for all integers k from 1 up to m, we now prove it for m + 1. Setting x = mr and y = r we obtain f((m + 1)r) + f((m – 1)r) = 2[f(mr) + f(r)], and by the induction assumption, f((m + 1)r) + (m – 1)2f(r) = 2[m2f(r) + f(r)], or
f((m + 1)r) = [2m2 + 2 – (m2– 2m + 1)]f(r) = (m + 1)2f(r),
which proves that f(m·r) = m2 f(r) for all positive integers m, as desired.
It is easy to extend this result to negative integers: for any real number s, setting x = 0 and y = s we have f(s) + f(–s) = 2[0 + f(s)], whence f(s) = f(–s); that is, f(m·r) = m2f(r) for all integers m and real numbers r.
Finally, we replace m·r by n·mr/n (for n a nonzero integer) in the previous result to obtain m2f(r) = f(m·r) = f(n·m·r/n) = n2f(m·r/n), whence
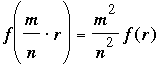
as claimed.
Our problem is the special case where r = 1, m = 22, and n = 7: f(22/7) = (22/7)2.
Comments. Our assumptions (i) and (ii) on f(x) put no constraint on its value when x is not rational (that is, when there exist no integers m and n for which x = m/n). For example, consider the number 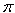 (that is, the ratio of the circumference of a circle to its diameter). Even though π and 22/7 are nearly equal, we know that because it is irrational, (that is, the ratio of the circumference of a circle to its diameter). Even though π and 22/7 are nearly equal, we know that because it is irrational, 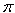 can not be reached from 1 in a finite number of steps using sums, differences, products, and quotients as we did for 22/7 in our first solution above; consequently f( can not be reached from 1 in a finite number of steps using sums, differences, products, and quotients as we did for 22/7 in our first solution above; consequently f(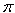 ) can be assigned any value whatsoever without violating either (i) or (ii). In other words, to extend our result that f(x) = x2 to all real numbers x, we would have to postulate some additional property such as continuity. It is easy to prove that the only continuous function that satisfies (i) and (ii) is the function f(x) = x2. In his solution Mangal assumed further that f(x) is differentiable for all x; he then showed how it follows immediately from property (i) that f '(x) satisfies the Cauchy functional equation (that we discuss next). ) can be assigned any value whatsoever without violating either (i) or (ii). In other words, to extend our result that f(x) = x2 to all real numbers x, we would have to postulate some additional property such as continuity. It is easy to prove that the only continuous function that satisfies (i) and (ii) is the function f(x) = x2. In his solution Mangal assumed further that f(x) is differentiable for all x; he then showed how it follows immediately from property (i) that f '(x) satisfies the Cauchy functional equation (that we discuss next).
Property (i) is an example of a functional equation; that is, it is an equation in which the indeterminate is a function. Functional equations arise naturally in many applications; they were first studied in the 18th century to solve physics problems. The first systematic investigation was by Cauchy in his famous treatise, Cours d'analyse de l'École Polytechnique, published in 1821. There he treated what is now referred to as the four fundamental Cauchy equations; the best known of these equations is f(x + y) = f(x) + f(y), whose only continuous solution over the reals is f(x) = kx, for some constant k. Its story can be found in introductory books about functional equations such as
J. Aczel, Lectures on Functional Equations and their Applications (Academic Press, 1966).
Wikipedia also has a nice discussion under the title "Cauchy functional equation":
http://en.wikipedia.org/wiki/Cauchy%27s_functional_equation.
Both Matthew Lim and Aditya Prasad looked at the problem of determining the most general function that satisfies our equations (i) and (ii). For that one needs the concept of a Hamel basis H: for every real number r there is a unique set of a finite number n of real numbers rj in H and of rational numbers qj such that
r = q1r1 + q2r2 + ... + qnrn.
In fact, Hamel devised his basis in 1905 to answer the analogous question about Cauchy's functional equation. See the Wikipedia article for more details. The construction of a Hamel basis is not at all elementary; it requires the axiom of choice. For our functional equation Lim and Prasad found that for any numbers u and v in the Hamel basis, one can arbitrarily assign the values f(u), f(v), and f(u + v). (We arbitrarily assigned the value f(1) = 1 to make the answer to our problem unique. Had we wished, we could have replaced (ii) by f(√2) = 2009, and requested the value of f((22√2)/7), which is 2009·(22/7)2 according to our second solution above.) For those readers interested in the details, we have a link to Lim's argument.
|

