|
MP12: August 2001
- You are given five points in the plane and are told that they are the midpoints of the edges of some pentagon. Find the pentagon.
- Given the midpoints of the sides of an n-gon in the plane, is it always possible to determine the n-gon?
MP11: July 2001
An old edition of Ripley's Believe It Or Not states that the number
N = 526315789473684210
is a persistent number: if N is multiplied by any positive integer, the resulting product always contains all ten digits 0, 1, 2, ..., 9 (with repetitions, of course).
- Prove or disprove Ripley's statement.
- Are there any persistent numbers that are smaller than N?
MP10: June 2001
We found this month's problem in Crux Mathematicorum 27:3 (April 2001) pages 204-205 - it is problem 3 from the Ninth Annual Konhauser Problemfest (Carleton College, prepared by David Savitt and Russell Mann.
a. |
Begin with a string of 10 A's, B's, and C's, as for example
A B C C B A B C B A.
Underneath, form a new row of length 1 less as follows: between two consecutive letters that are different you write the third letter, and between two letters that are the same, you write the same letter again. Repeat this process until you have only one letter in the new row. For example, for the string given above you will have
A B C C B A B C B A
C A C A C C A A C
B B B B C B A B
B B B A A C C
B B C A B C
B A B C A
C C A B
C B C
A A
A
Prove that the letters at the corners of the resulting triangle are always either all the same or all different. |
| b. |
For which numbers n (besides 10) is the result from part (a) true for all strings of n A's, B's, and C's? |
MP9: May 2001
MP8: April 2001
The square with vertices (0, 0), (1, 0), (1, 1), (0, 1) has two properties that are of interest here:
- all its vertices have integer coordinates (so we call them lattice points),
- except for the vertices, no point on the boundary or in the interior is a lattice point.
This is not the case, for example, for the square with vertices (0, 0), (2, 0), (2, 2), (0, 2); although its vertices are lattice points, there are several lattice points (such as (0, 1)) on the boundary , and even an interior lattice point (1, 1). On the other hand, it is easy to find convex quadrangles with vertices at lattice points that contain no lattice points -- it just has to be long and thin, such as (0, 0), (1, 2), (2, 5), (1, 3). (We call a polygon convex if its boundary has no indentations; more precisely, line segments that join two of its vertices must contain no exterior points.)
Is there a convex pentagon with lattice points as vertices that contains no other lattice points either inside or on the boundary?
MP7: March 2001
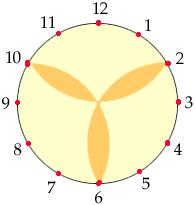
The diagram shows a unit circle with the boundary of the shaded portion consisting of three circular arcs of radius 1 whose centres are equally spaced on the surrounding circle. (If you imagine the diagram to be a clock's face, the centres are at 12:00, 4:00, and 8:00.) The problem is to dissect the unshaded portion of the clock's face into pieces that can be reassembled to form a rectangle. |
MP6: February 2001
This month we have a variation on a well-known problem: It is easy to cover all the squares of an ordinary (8 by 8) chessboard using 32 dominoes; however, if we remove the squares from two opposite corners of the chessboard, the resulting grid cannot be covered with 31 dominoes. If you have not seen this classic problem before, you may wish to try solving it as a warm-up exercise to our problem.Consider a tetromino consisting of four squares arranged in a T as follows:

It is easy to cover the 8 by 8 chessboard with these tetrominoes.
Is it also possible to cover a 10 by 10 board with t-shaped tetrominoes? Either show how to do it, or prove that it cannot be done. |
MP5: January 2001
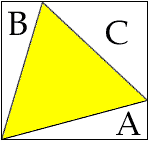
An equilateral triangle is inscribed in, and has a common vertex with, a rectangle. If A, B, C are the areas of the complementary right triangles (as shown in the figure), prove that A + B = C.
|
MP4: December 2000
The counting numbers are partitioned into the groups
(1), (2, 3), (4, 5, 6), (7, 8, 9, 10), (11, 12, 13, 14, 15), ... .
Find the sum of the numbers in the nth group.
|
MP3: November 2000
|
How many faces can a polyhedron have if all those faces are triangles?
Some background information. A polyhedron is a solid figure with flat sides (called faces). In general each of those sides would be a polygon, but for our problem they are triangles. Most of you are probably familiar with the three examples whose faces are equilateral triangles, namely the tetrahedron (4 faces), octahedron (8 faces), and icosahedron (20 faces). In this problem there is no requirement that the triangular faces be equilateral.
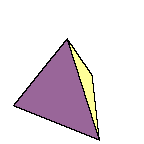  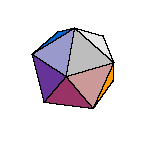
|
MP2: October 2000
Here is something you can do with a crossword puzzle even when you don't know any words. You start with a grid consisting mostly of white squares, but with some of them black. We say that two squares are neighbours if they share an entire edge. Start filling in the white squares that have at least two neighbours already black.For example, with
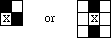
we would fill in the square labelled X, because in each case it has two black neighbours. The new black squares allow you to fill in other squares; after a while you either fill in the whole grid, or you end up with a bunch of white squares that are adjacent to at most one black square. Our problem deals with the possibility of making an entire 8 by 8 grid all black. For instance, suppose that your original configuration is an 8 by 8 grid with the black squares down the main diagonal:
 |
leading
to |
 |
and eventually
to |
 |
Of course, there are many initial configurations of eight black squares that lead to a completely filled in 8 by 8 grid, such as
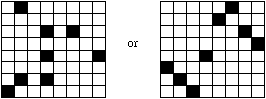
Does there exist a configuration of 7 black squares that will allow one to completely fill in an 8 by 8 grid, or does one always need at least 8 black squares in the original configuration to do that?
|
MP1: September 2000
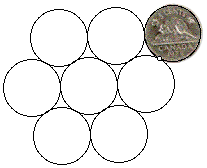 |
Eight nickels are touching as in the figure. If the upper right nickel (fully drawn) is rolled, without slipping, around the other seven, how many complete somersaults will the beaver make as it rolls through one full circuit of the array? |
|

